Theorema egregium
O Theorema Egregium de Gauss (Latim para "Notável Teorema") é um resultado importante da geometria diferencial comprovada por Carl Friedrich Gauss. O teorema é sobre a curvatura das superfícies. O teorema afirma que a curvatura pode ser determinada medindo ângulos, distâncias e suas taxas apenas em uma superfície. Não há necessidade de falar sobre a forma particular em que a superfície está embutida no espaço Euclidiano tridimensional circundante. Em outras palavras, a curvatura gaussiana de uma superfície não muda se alguém dobrar a superfície sem esticá-la.
Gauss apresentou o teorema desta maneira (traduzido do latim):
Por esta razão, a fórmula do artigo anterior leva ao notável Teorema. Se uma superfície curva é desenvolvida em qualquer outra superfície qualquer, a medida da curvatura em cada ponto permanece inalterada.
O teorema é "notável" porque a definição inicial da curvatura gaussiana faz uso direto da posição da superfície no espaço. Portanto, é bastante surpreendente que o resultado não dependa de sua incorporação, apesar de todas as deformações de flexão e torção sofridas.
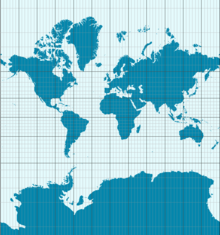
Uma conseqüência do Theorema Egregium é que a Terra não pode ser exibida em um mapa sem distorção. A projeção de Mercator, mostrada aqui, preserva os ângulos, mas muda a área. Como exemplo, a Antártida é mostrada muito maior do que realmente é.
Perguntas e Respostas
Q: O que é o Theorema Egregium de Gauss?
R: O Teorema Egregium de Gauss é um resultado importante da geometria diferencial que trata da curvatura de superfícies, provado por Carl Friedrich Gauss.
P: Como a curvatura pode ser determinada, de acordo com o Teorema Egregium de Gauss?
R: De acordo com o Teorema Egregium de Gauss, a curvatura pode ser determinada medindo-se ângulos, distâncias e suas taxas apenas em uma superfície.
P: É necessário falar sobre a maneira específica pela qual a superfície está inserida no espaço euclidiano tridimensional circundante para determinar a curvatura?
R: Não, não é necessário falar sobre a maneira específica pela qual a superfície está inserida no espaço euclidiano tridimensional circundante para determinar a curvatura de acordo com o Teorema Egregium de Gauss.
P: A curvatura gaussiana de uma superfície muda se a superfície for dobrada sem ser esticada?
R: Não, a curvatura gaussiana de uma superfície não se altera se a superfície for dobrada sem ser esticada, de acordo com o Teorema Egregium de Gauss.
P: Quem apresentou o teorema dessa maneira?
R: Gauss apresentou o teorema dessa maneira.
P: Por que o teorema é notável?
R: O teorema é "notável" porque a definição inicial da curvatura gaussiana faz uso direto da posição da superfície no espaço. Portanto, é bastante surpreendente que o resultado não dependa de sua incorporação, apesar de todas as deformações de flexão e torção sofridas.
P: De que maneira Gauss apresentou o teorema?
R: Gauss apresentou o teorema de tal forma que, se uma superfície curva for desenvolvida em qualquer outra superfície, a medida da curvatura em cada ponto permanecerá inalterada.
Pesquise na enciclopédia