Correlação
Em estatística e teoria da probabilidade, correlação significa o quanto dois conjuntos de dados estão intimamente relacionados.
A correlação nem sempre significa que uma causa a outra. É muito possível que haja um terceiro fator envolvido.
A correlação geralmente tem uma das duas direções. Estas são positivas ou negativas. Se for positiva, então os dois conjuntos sobem juntos. Se for negativo, então um sobe enquanto o outro desce.
Muitas medidas diferentes de correlação são usadas para diferentes situações. Por exemplo, em um gráfico de dispersão, as pessoas desenham uma linha de melhor ajuste para mostrar a direção da correlação.
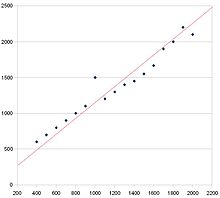
Este gráfico de dispersão tem correlação positiva. Você pode dizer porque a tendência está em alta e certa. A linha vermelha é uma linha de melhor ajuste.
Correlação explicativa
Fortes e fracos são palavras usadas para descrever correlação. Se há correlação forte, então os pontos estão todos próximos uns dos outros. Se há uma correlação fraca, então os pontos estão todos separados. Há maneiras de fazer com que os números mostrem quão forte é a correlação. Estas medidas são chamadas de coeficientes de correlação. O mais conhecido é o coeficiente de correlação produto-momento de Pearson. Você coloca os dados em uma fórmula e ela lhe dá um número. Se o número for 1 ou -1, então há uma forte correlação. Se a resposta for 0, então não há correlação. Outro tipo de coeficiente de correlação é o coeficiente de correlação de classificação da Spearman.
Correlação vs. causalidade
A correlação nem sempre significa que uma coisa causa a outra (causalidade), porque algo mais poderia ter causado ambas. Por exemplo, em dias quentes as pessoas compram sorvete, e as pessoas também vão à praia onde alguns são comidos por tubarões. Há uma correlação entre a venda de sorvete e os ataques de tubarões (ambos sobem conforme a temperatura sobe neste caso). Mas só porque a venda de sorvete sobe, não significa que a venda de sorvete cause (causa) mais ataques de tubarões ou vice-versa.
Porque a correlação não implica em causalidade, cientistas, economistas, etc. testarão suas teorias criando ambientes isolados onde apenas um fator é mudado (onde isto é possível). No entanto, políticos, vendedores, agências de notícias e outros freqüentemente sugerem que uma correlação particular implica em uma causalidade. Isto pode ser devido à ignorância ou ao desejo de persuadir. Assim, um noticiário pode atrair a atenção dizendo que as pessoas que consomem um determinado produto com mais freqüência têm um problema de saúde particular, implicando em uma causa que poderia ser realmente devida a outra coisa.
Páginas relacionadas
- Cohen, J., Cohen P., West, S.G., & Aiken, L.S. (2003). Aplicou a análise de regressão/correlação múltipla para as ciências comportamentais. (3ª ed.) Hillsdale, NJ: Lawrence Erlbaum Associates.
Perguntas e Respostas
P: O que é correlação?
R: Correlação é uma forma de indicar a proximidade entre dois conjuntos de dados.
P: A correlação significa que um conjunto de dados causa o outro?
R: Não, a correlação nem sempre significa que um conjunto de dados causa o outro. De fato, geralmente há um terceiro fator envolvido.
P: Quais são as duas direções da correlação?
R: As duas direções da correlação são positiva e negativa.
P: O que significa uma correlação positiva?
R: Uma correlação positiva significa que os dois conjuntos de dados aumentam juntos.
P: O que significa uma correlação negativa?
R: Uma correlação negativa significa que um conjunto de dados sobe enquanto o outro desce.
P: Existem diferentes medidas de correlação?
R: Sim, muitas medidas diferentes de correlação são usadas em diferentes situações.
P: Como as pessoas geralmente mostram a direção da correlação em um gráfico de dispersão?
R: As pessoas geralmente desenham uma linha de melhor ajuste para mostrar a direção da correlação em um gráfico de dispersão.
Pesquise na enciclopédia