Conjunto

Um conjunto é uma idéia da matemática. Um conjunto tem membros (também chamados de elementos). Um conjunto é fixado por seus membros. É o único conjunto que tem os mesmos membros (se o conjunto X e o conjunto Y têm os mesmos membros, então X = Y). Um conjunto não pode ter o mesmo membro mais de uma vez. A filiação é a única coisa que significa alguma coisa. Por exemplo, não há nenhuma ordem ou outra distinção entre os membros. Um conjunto em particular é o "conjunto vazio" (também chamado de conjunto nulo). O conjunto vazio não tem membros. Qualquer coisa pode ser um membro de um conjunto. Um conjunto pode ser um membro de um conjunto. (Se um conjunto é um membro de si mesmo, tome cuidado com o paradoxo de Russell).

Georg Cantor, em 1894. Cantor foi o primeiro matemático a falar sobre conjuntos

A definição original de um conjunto do Cantor: Por um conjunto (...) devemos entender qualquer coleção em um todo (...) M de objetos m definidos e separados de nossa intuição ou de nosso pensamento. Estes objetos são chamados os elementos de M.

Notação

A maioria dos matemáticos usa letras maiúsculas em itálico (geralmente romanas) para escrever sobre conjuntos. As coisas que são vistas como elementos de conjuntos são geralmente escritas com letras minúsculas romanas.

Uma maneira de mostrar um conjunto é através de uma lista de seus membros, separados por vírgulas, incluídos em aparelho. Por exemplo,

X={1,2,3} é definido que tem membros 1, 2, e 3.

Outra forma é através de uma declaração do que é verdade sobre os membros do conjunto, como esta:

{x | x é um número natural & x < 4}.

Em inglês falado, ou seja: "o conjunto de todos os x tais que x é um número natural e x é menos de quatro".

O conjunto vazio é escrito de uma maneira especial:

∅ $\emptyset$

Quando o objeto a é membro do conjunto A, ele é escrito como:

$a$ $\in$ $A$ .

Em inglês falado, ou seja: "a é um membro de A".

O que fazer com os conjuntos

Elemento de

Várias coisas podem ser colocadas em uma bolsa. Mais tarde, uma pergunta válida seria se uma determinada coisa está na sacola. Os matemáticos chamam este elemento de. Algo é um elemento de um conjunto, se essa coisa puder ser encontrada na respectiva bolsa. O símbolo usado para isso é ∈ em estilo de jogo. $\in$

a ∈ Um estilo de jogo em matemática. } $a\in \mathbf {A}$

significa que um "estilo de jogoa" está na sacola Um "estilo de jogo a" está na sacola Um "estilo de jogo a } $\mathbf {A}$

Conjunto vazio

Como uma bolsa, um conjunto também pode estar vazio. O conjunto vazio é como um saco vazio: não tem nada dentro dele.

Comparação de conjuntos

Dois conjuntos podem ser comparados. Isto é como olhar para duas bolsas diferentes. Se elas contêm as mesmas coisas, elas são iguais.

Cardinalidade de um conjunto

Quando os matemáticos falam de um conjunto, eles às vezes querem saber o tamanho de um conjunto. Eles fazem isso contando quantos elementos estão no conjunto (quantos itens estão na bolsa). A cardinalidade pode ser um número simples. O conjunto vazio tem uma cardinalidade de 0. O conjunto { a p l e , o r a n g e } O estilo de jogo $\{apple,orange\}$ tem uma cardinalidade de 2.

Dois conjuntos têm a mesma cardinalidade se conseguirmos emparelhar seus elementos - se conseguirmos unir dois elementos, um de cada conjunto. O conjunto { a p l e , o r a n g e } $\{apple,orange\}$ e o conjunto, m o o n $\{sun,moon\}$ têm a mesma cardinalidade. Podemos emparelhar maçã com sol, e laranja com lua. A ordem não importa. É possível emparelhar os elementos, e nenhum é deixado de fora. Mas o conjunto {d o g , c a t , b i r d } $\{dog,cat,bird\}$ e o conjunto 5 , 6 $\{5,6\}$ têm uma cardinalidade diferente. Se tentarmos emparelhá-los, sempre deixamos de fora um animal.

Cardealinidade infinita

Às vezes, a cardinalidade não é um número. Às vezes, um conjunto tem uma cardinalidade infinita. O conjunto de números inteiros é um conjunto com uma cardinalidade infinita. Alguns conjuntos com uma cardinalidade infinita são maiores (têm uma cardinalidade maior) do que outros. Há mais números reais do que números naturais, por exemplo. Isso significa que não podemos emparelhar o conjunto de números inteiros e o conjunto de números reais, mesmo que tenhamos trabalhado para sempre. Se um conjunto tem a mesma cardinalidade que o conjunto de números inteiros, é chamado de conjunto de números inteiros contáveis. Mas se um conjunto tem a mesma cardinalidade que os números reais, ele é chamado de conjunto incontável.

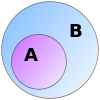
Subconjuntos

Se você olhar para o conjunto {a,b} e o conjunto {a,b,c,d}, você pode ver que todos os elementos do primeiro conjunto também estão no segundo conjunto.
Nós dizemos: {a,b} é um subconjunto de {a,b,c,d}como
uma fórmula parecida com esta:
a , b ⊆ { a , b , c , d } estilo de jogo a, b, subseteq a, b, c, d $\{a,b\}\subseteq \{a,b,c,d\}$

Quando todos os elementos de A são também elementos de B, chamamos de A um subconjunto de B:
A ⊆ B {\displaystyle A`subseteq B} $A\subseteq B$
Costuma-se ler "A está contido em B".

Exemplo:
todo Chevrolet é um carro americano. Portanto, o conjunto de todos os Chevrolets está contido no conjunto de todos os carros americanos.

Operações de conjunto

Há diferentes maneiras de combinar conjuntos.

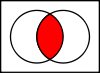
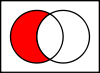
Intersecções

A interseção A ∩ B {\displaystyle A\cap B} $A\cap B$ de dois conjuntos A e B é um conjunto que contém todos os elementos,
que estão tanto no conjunto A quanto no conjunto B.
Quando A é o conjunto de todos os carros baratos, e B é o conjunto de todos os carros americanos,
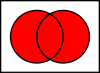
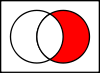
então A ∩ B $A\cap B$ é o conjunto de todos os carros americanos baratos.

Sindicatos

A união A ∪ B {\i1} $A\cup B$ de dois conjuntos A e B é um conjunto que contém todos os elementos,
que estão no conjunto A ou no conjunto B.

Este "ou" é a disjunção inclusiva, portanto, o sindicato contém também os elementos, que estão no conjunto A e no conjunto B.

A propósito: Isto significa, que o cruzamento é um subconjunto do sindicato:

( A ∩ B ) ⊆ ( A ∪ B ) {\i1}displaystyle (A\i}cap B){\i}subseteq (A\i}cup B)} $(A\cap B)\subseteq (A\cup B)$

Quando A é o conjunto de todos os carros baratos, e B é o conjunto de todos os carros americanos,
então A ∪ B {\i1} $A\cup B$ é o conjunto de todos os carros, sem todos os carros caros que não são da América.

Complementos

O complemento pode significar duas coisas diferentes:

O complemento de A é o universo U sem todos os elementos de A:

A C = U ∖ A ^{\\rm ^{\C}}=U=U=setminus A} $A^{\rm {C}}=U\setminus A$
O universo U é o conjunto de todas as coisas sobre as quais você fala.
Quando U é o conjunto de todos os carros, e A é o conjunto de todos os carros baratos,
então ^AC é o conjunto de todos os carros caros.

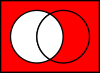
O complemento relativo de A em B é o conjunto B sem todos os elementos de A:

B ∖ A {\i1}displaystyle B{\i1}setminus A $B\setminus A$
Muitas vezes é chamada de diferença de conjunto.
Quando A é o conjunto de todos os carros baratos, e B é o conjunto de todos os carros americanos,
então B ∖ A $B\setminus A$ {\i1}é o conjunto de todos os carros americanos caros.

Se você trocar os conjuntos na diferença do conjunto, o resultado é diferente:
no exemplo com os carros, a diferença A ∖ B {\i1} $A\setminus B$ é o conjunto de todos os carros baratos, que não são feitos na América.

A ⊆ B {\i1}displaystyle A{\i}subseteq B $A\subseteq B$

A ∩ B {\displaystyle A{\displaystyle A{\displaystyle A{\displaystyle B} $A\cap B$

A ∪ B {\i1}b {\i1}displaystyle A $A\cup B$

A C = U ∖ A ^{\\rm ^{\C}}=U=U=setminus A} $A^{\rm {C}}=U\setminus A$

B ∖ A {\i1}displaystyle B{\i1}setminus A $B\setminus A$

A ∖ B {\i1}displaystyle A{\i1}setminus B $A\setminus B$

Conjuntos especiais

Alguns conjuntos são muito importantes para a matemática. Eles são usados com muita freqüência. Um deles é o conjunto vazio. Muitos destes conjuntos são escritos usando quadro negro em negrito, como mostrado abaixo. Os conjuntos especiais incluem:

P {\i1}estilo de exibição {P}mathbb } $\mathbb {P}$ , denotando o conjunto de todos os primes.
N estilo de jogo {\i1}mathbb {N } $\mathbb {N}$ , denotando o conjunto de todos os números naturais. Ou seja, ao estilo Nmathbb. } $\mathbb {N}$ = {1, 2, 3, ...{1, 2, 3, ...ou às vezes ao estilo Nmathbb {N} } $\mathbb {N}$ = {0, 1, 2, 3, ...}.
Z estilo de jogo Z } $\mathbb {Z}$ , denotando o conjunto de todos os números inteiros (seja positivo, negativo ou zero). Portanto, o Z é ao estilo Zmathbb. } $\mathbb {Z}$ = {..., -2, -1, 0, 1, 2, ...}.
P Estilo de jogo Mathbb } $\mathbb {Q}$ A partir de então, o conjunto de todos os números racionais (ou seja, o conjunto de todas as frações adequadas e impróprias). Assim, Q = { a b : a , b ∈ Z , b ≠ 0 } estilo de jogomathbb = esquerda esquerdabeginmatrixfracfrac a,bbmathbb b) 0,1,1} $\mathbb {Q} =\left\{{\begin{matrix}{\frac {a}{b}}\end{matrix}}:a,b\in \mathbb {Z} ,b\neq 0\right\}$ Por exemplo, 1 4 ∈ Q estilo de exibição begin (matriz) frac (1) frac (4) end ${\begin{matrix}{\frac {a}{b}}\end{matrix}}$ (matriz) em mathbbb (Q) ${\begin{matrix}{\frac {1}{4}}\end{matrix}}\in \mathbb {Q}$ e 11 6 6 ∈ Q Q estilo de jogobegin (matriz) frac (11) end (matriz) inmathbb (Q) } ${\begin{matrix}{\frac {11}{6}}\end{matrix}}\in \mathbb {Q}$ . Todos os números inteiros estão neste conjunto, já que cada número inteiro a pode ser expresso como a fração de um jogo ao estilo de uma matriz. ${\begin{matrix}{\frac {a}{1}}\end{matrix}}$ .
R estilo de jogo de matemática $\mathbb {R}$ , denotando o conjunto de todos os números reais. Este conjunto inclui todos os números racionais, juntamente com todos os números irracionais (isto é, números que não podem ser reescritos como frações, tais como π , {\i1}displaystyle $\pi ,$ e , {\i1}displaystyle e,} $e,$ e √2).
C {\i1}displaystyle {\i}mathbb } $\mathbb {C}$ , denotando o conjunto de todos os números complexos.

Cada um desses conjuntos de números tem um número infinito de elementos, e P ⊂ N ⊂ Z ⊂ Q ⊂ R ⊂ C {\i1}displaystyle {\i}mathbb {P \Subconjunto \Subconjunto \Subconjunto \Subconjunto Subconjunto Subconjunto Subconjunto Subconjunto Subconjunto } $\mathbb {P} \subset \mathbb {N} \subset \mathbb {Z} \subset \mathbb {Q} \subset \mathbb {R} \subset \mathbb {C}$ . Os primes são utilizados com menos freqüência que os outros fora da teoria dos números e campos relacionados.

Paradoxos sobre conjuntos

O matemático BertrandRussell descobriu que existem problemas com esta teoria de conjuntos. Ele afirmou isso em um paradoxo chamado paradoxo de Russell. Uma versão mais fácil de entender, mais próxima da vida real, é chamada de paradoxo do barbeiro:

O paradoxo do barbeiro

Há uma pequena cidade em algum lugar. Nessa cidade, há um barbeiro. Todos os homens da cidade não gostam de barba, então ou eles se barbeam ou vão ao barbeiro para serem barbeados pelo barbeiro.

Podemos, portanto, fazer uma declaração sobre o próprio barbeiro: O barbeiro barbeia todos os homens que não se depilam. Ele só barbeia esses homens (já que os outros se barbeam a si mesmos e não precisam de um barbeiro para fazer a barba).

Isto, é claro, levanta a questão: O que o barbeiro faz todas as manhãs para parecer barbeado e limpo? Este é o paradoxo.

Se o barbeiro não se barbear, ele seguirá a regra e se barbeará (vá até a barbearia para fazer a barba)
Se o barbeiro de fato se barbear, ele não se barbeará, de acordo com a regra dada acima.

Perguntas e Respostas

P: O que é um conjunto?

R: Um conjunto é uma idéia da matemática. É composto de membros (também chamados de elementos) que são definidos por seus membros, portanto, quaisquer dois conjuntos com os mesmos membros são os mesmos.

P: Um conjunto pode ter o mesmo membro mais de uma vez?

R: Não, um conjunto não pode ter o mesmo membro mais de uma vez.

P: A ordem é importante em um conjunto?

R: Não, a ordem não tem importância em um conjunto. Qualquer coisa pode ser um membro de um conjunto, inclusive os próprios conjuntos.

P: O que acontece se um conjunto for um membro de si mesmo?

R: Se um conjunto é um membro de si mesmo, paradoxos como o de Russell podem acontecer.

P: A afiliação é a única coisa que importa para os conjuntos?

R: Sim, a afiliação é a única coisa que importa para os conjuntos.

P: Como o senhor sabe se dois conjuntos são iguais?

R: Dois conjuntos são iguais se eles têm os mesmos membros.