Matemática

A matemática é o estudo de números, formas e padrões. A palavra vem da palavra grega "μάθημα" (máthema), que significa "ciência, conhecimento ou aprendizagem", e às vezes é abreviada para matemática (na Inglaterra, Austrália, Irlanda e Nova Zelândia) ou matemática (nos Estados Unidos e Canadá). As palavras curtas são freqüentemente usadas para aritmética, geometria ou álgebra simples pelos estudantes e suas escolas.

A matemática inclui o estudo de:

Números: como as coisas podem ser contadas.
Estrutura: como as coisas são organizadas. Este subcampo é normalmente chamado de álgebra.
Local: onde as coisas estão e sua disposição. Este subcampo é normalmente chamado de geometria.
Mudança: como as coisas se tornam diferentes. Este subcampo é normalmente chamado de análise.

A matemática é útil para resolver problemas que ocorrem no mundo real, tantas pessoas além dos matemáticos estudam e utilizam a matemática. Hoje em dia, alguma matemática é necessária em muitos trabalhos. As pessoas que trabalham em negócios, ciência, engenharia e construção precisam de algum conhecimento de matemática.

Resolução de problemas em matemática

A matemática resolve os problemas usando a lógica. Uma das principais ferramentas de lógica utilizadas pelos matemáticos é a dedução. A dedução é uma forma especial de pensar para descobrir e provar novas verdades usando verdades antigas. Para um matemático, a razão pela qual algo é verdadeiro (chamada de prova) é tão importante quanto o fato de ser verdade, e esta razão é muitas vezes encontrada usando a dedução. O uso da dedução é o que torna o pensamento matemático diferente de outros tipos de pensamento científico, que pode depender de experimentos ou de entrevistas.

A lógica e o raciocínio são usados pelos matemáticos para criar regras gerais, que são uma parte importante da matemática. Estas regras deixam de fora informações que não são importantes para que uma única regra possa cobrir muitas situações. Ao encontrar regras gerais, a matemática resolve muitos problemas ao mesmo tempo em que estas regras podem ser usadas em outros problemas. Estas regras podem ser chamadas de teoremas (se tiverem sido provadas) ou conjecturas (se ainda não se souber se são verdadeiras). A maioria dos matemáticos utiliza raciocínios não lógicos e criativos a fim de encontrar uma prova lógica.

Às vezes, a matemática encontra e estuda regras ou idéias que ainda não entendemos. Muitas vezes, na matemática, as idéias e as regras são escolhidas porque são consideradas simples ou limpas. Por outro lado, às vezes estas idéias e regras são encontradas no mundo real depois que são estudadas em matemática; isto já aconteceu muitas vezes no passado. Em geral, o estudo das regras e idéias da matemática pode nos ajudar a entender melhor o mundo. Alguns exemplos de problemas matemáticos são adição, subtração, multiplicação, divisão, cálculo, frações e decimais. Os problemas de álgebra são resolvidos através da avaliação de certas variáveis. Uma calculadora responde a cada problema matemático nas quatro operações aritméticas básicas.

Áreas de estudo em matemática

Número

A matemática inclui o estudo de números e quantidades. É um ramo da ciência que lida com a lógica da forma, quantidade e disposição. A maioria das áreas listadas abaixo são estudadas em muitos campos diferentes da matemática, incluindo teoria de conjuntos e lógica matemática. O estudo da teoria dos números geralmente se concentra mais na estrutura e comportamento dos inteiros do que nos fundamentos reais dos números em si, e por isso não está listado nesta subseção.

0 , 1 , 2 , 3 , ... {\i1}displaystyle 0,1,2,3,{\i1}ldots $0,1,2,3,\ldots$	... , - 1 , 0 , 1 , ... {\i1}displaystyle {\i1}ldots ,-1,0,1,{\i}ldots $\ldots ,-1,0,1,\ldots$	1 2 , 2 3 , 0,125 , ... {\i1},0,125,{\i1}ldots {\i1}displaystyle {\i1},0,125,{\i}ldots {\i1} ${\frac {1}{2}},{\frac {2}{3}},0.125,\ldots$	π , e , 2 , ... {\i1}, e,{\i1},{\i1}ldots {\i1} $\pi ,e,{\sqrt {2}},\ldots$	1 + i , 2 e i π / 3 , ... {\i1}displaystyle 1+i,2e^{i\i /3},{\i}ldots $1+i,2e^{i\pi /3},\ldots$
Números naturais	Integers	Números racionais	Números reais	Números complexos
0 , 1 , ... , ω , ω + 1 , ... , 2 ω , ... {\i1}displaystyle 0,1,1,ldots ,{\i1}omega ,{\i1,{\i1}ldots ,{\i1}2,{\i1}ldots $0,1,\ldots ,\omega ,\omega +1,\ldots ,2\omega ,\ldots$	ℵ 0 , ℵ 1 , ... {\i1}displaystyle {0},}aleph _{1},{1}ldots } $\aleph _{0},\aleph _{1},\ldots$	+ , - , × , ÷ estilo de jogo +,-,-,tempos,iv $+,-,\times ,\div$	> , ≥ , = , ≤ , < {\i1}displaystyle >,{\i}geq ,=,{\i}leq ,< } $>,\geq ,=,\leq ,<$	f ( x ) = x {\f(x)={\f(x)={\f(x)}}} $f(x)={\sqrt {x}}$
Números ordinais	Números cardeais	Operações aritméticas	Relações aritméticas	Funções

Estrutura

Muitas áreas da matemática estudam a estrutura que um objeto tem. A maioria dessas áreas faz parte do estudo da álgebra.


Teoria dos números	Álgebra abstrata	Álgebra linear	Teoria dos pedidos	Teoria dos gráficos

Forma

Algumas áreas da matemática estudam as formas das coisas. A maioria dessas áreas faz parte do estudo da geometria.


Topologia	Geometria	Trigonometria	Geometria diferencial	Geometria fractal

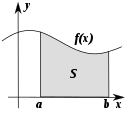
Mudança

Algumas áreas da matemática estudam a forma como as coisas mudam. A maioria dessas áreas faz parte do estudo de análise.


Cálculo	Cálculo vetorial	Análise

Equações diferenciais	Sistemas dinâmicos	Teoria do caos

Matemática aplicada

A matemática aplicada utiliza a matemática para resolver problemas de outras áreas, como engenharia, física e computação.

Análise numérica - Otimização - Teoria da probabilidade - Estatística - Finanças matemáticas - Teoria dos jogos - Física matemática - Dinâmica dos fluidos - Algoritmos computacionais

Teoremas famosos

Estes teoremas têm matemáticos interessados e pessoas que não são matemáticos.

Teorema de Pitágoras - O último teorema de Fermat - Conjectura de Goldbach - Conjectura de Twin Prime - Teoremas de Gödel incompletos - Conjectura de Poincaré - Argumento diagonal de Cantor - Teorema de quatro cores - Lema de Zorn - Identidade de Euler - Tese de Igreja-Tura

Estes são teoremas e conjecturas que mudaram muito a matemática.

Hipótese de Riemann - Hipótese Continuum - P versus NP - Teorema de Pitágoras - Teorema do limite central - Teorema fundamental do cálculo - Teorema fundamental da álgebra - Teorema fundamental da aritmética - Teorema fundamental da geometria projetiva - Teorema da classificação de superfícies - Teorema de Gauss-Bonnet - O último teorema de Fermat - Teorema de Kantorovich

Fundamentos e métodos

Os progressos na compreensão da natureza da matemática também influenciam a forma como os matemáticos estudam seu assunto.

Filosofia da Matemática - Intuicionismo matemático - Construtivismo matemático - Fundamentos da matemática - Teoria dos conjuntos - Lógica simbólica - Teoria dos modelos - Teoria das categorias - Lógica - Matemática inversa - Tabela de símbolos matemáticos

A história e o mundo dos matemáticos

A matemática na história, e a história da matemática.

História da matemática - Linha do tempo da matemática - Matemáticos - Medalha de campo - Prêmio Abel - Millennium Prize Problems (PrêmioMatemática do Milênio) - International Mathematical Union - Concursos de Matemática - Pensamento lateral - Matemática e gênero

Prêmios em Matemática

Não há prêmio Nobel em matemática. Os matemáticos podem receber o prêmio Abel e a Medalha Fields por trabalhos importantes.

O Clay Mathematics Institute disse que dará um milhão de dólares a qualquer um que resolva um dos problemas do Prêmio Millennium.

Ferramentas matemáticas

Há muitas ferramentas que são usadas para fazer matemática ou para encontrar respostas a problemas matemáticos.

Ferramentas mais antigas

Ábaco
Ossos de Napier, régua de cálculo
Régua e Bússola
Cálculo mental

Ferramentas mais recentes

Calculadoras e computadores
Linguagens de programação
Sistemas de álgebra computacional (listagem)
Notação resumida da Internet
software de análise estatística (por exemplo, SPSS)
Linguagem de programação SAS
Linguagem de programação R

Veja também

Linha do tempo das mulheres na matemática
Sociedade Americana de Matemática
Sociedade para a Matemática Industrial e Aplicada
Projeto de Genealogia Matemática
Classificação do Assunto Matemático

Perguntas e Respostas

P: O que é matemática?

R: A matemática é o estudo de números, formas e padrões. A palavra vem da palavra grega μάθημα (máthema), que significa "ciência, conhecimento ou aprendizagem".

P: Quais são as principais áreas da matemática?

R: As principais áreas da matemática são números, estrutura (álgebra), lugar (geometria) e mudança (análise).

P: Como é usada a matemática no mundo real?

R: A matemática aplicada é útil para resolver problemas do mundo real. As pessoas que trabalham em negócios, ciência, engenharia e construção usam a matemática.

P: Existe uma versão abreviada de "matemática"?

R: Sim - pode ser abreviado para "matemática" nos países da Commonwealth britânica ou "matemática" na América do Norte.

P: O que significa a palavra "matemática"?

R: A palavra "matemática" vem da palavra grega μάθημα (máthema), que significa "ciência, conhecimento ou aprendizagem".

P: Que tipo de solução de problemas envolve a matemática aplicada?

R: A matemática aplicada envolve a solução de problemas do mundo real que as pessoas que trabalham nos negócios, na ciência, na engenharia e na construção encontram.