Teorema de quatro cores
O teorema das quatro cores é um teorema da matemática. Ele diz que em qualquer superfície plana com regiões nela (as pessoas pensam nelas como mapas), as regiões podem ser coloridas com não mais do que quatro cores. Duas regiões que têm uma fronteira comum não devem ter a mesma cor. Elas são chamadas adjacentes (uma ao lado da outra) se compartilharem um segmento da fronteira, e não apenas um ponto.
Este foi o primeiro teorema a ser provado por um computador, em uma prova por exaustão. Na prova por exaustão, a conclusão é estabelecida dividindo-a em casos, e provando cada um separadamente. Pode haver muitos casos. Por exemplo, a primeira prova do teorema de quatro cores foi uma prova por exaustão com 1.936 casos. Esta prova foi controversa porque a maioria dos casos foi verificada por um programa de computador, e não manualmente. A prova mais curta conhecida do teorema das quatro cores ainda hoje tem mais de 600 casos.
Embora o problema tenha sido apresentado pela primeira vez como um problema para colorir mapas políticos de países, os cartógrafos não estão muito interessados no mesmo. De acordo com um artigo do historiador matemático Kenneth May (Wilson 2002, 2), "Os mapas que utilizam apenas quatro cores são raros, e aqueles que normalmente requerem apenas três". Os livros sobre cartografia e a história da elaboração de mapas não mencionam a propriedade de quatro cores".
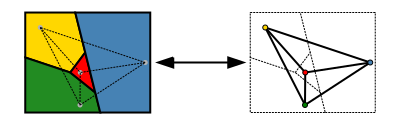
Muitos mapas mais simples podem ser coloridos usando três cores. A quarta cor é necessária para alguns mapas, como um em que uma região é cercada por um número ímpar de outras, que se tocam umas nas outras em um ciclo. Um desses exemplos é dado na imagem. O teorema das cinco cores afirma que cinco cores são suficientes para colorir um mapa. Ele tem uma prova curta e elementar e foi comprovado no final do século XIX. (Heawood 1890) Provando que quatro cores são tudo o que é necessário, revelou-se muito mais difícil. Muitas provas falsas e falsos contra-exemplos apareceram desde a primeira afirmação do teorema das quatro cores em 1852.

Três cores não são suficientes para colorir este mapa.

Exemplo de um mapa de quatro cores
Formulação exata do problema
Intuitivamente, o teorema das quatro cores pode ser declarado como "dada qualquer separação de um plano em regiões contíguas, chamadas de mapa, as regiões podem ser coloridas usando no máximo quatro cores para que não haja duas regiões adjacentes que tenham a mesma cor". Para poder resolver o problema corretamente, é necessário esclarecer alguns aspectos: Primeiro, todos os pontos que pertencem a três ou mais países devem ser ignorados. Em segundo lugar, mapas bizarros com regiões de área finita e perímetro infinito podem exigir mais de quatro cores.
Para o propósito do teorema, todo "país" tem que ser uma região simplesmente conectada, ou contígua. No mundo real, isto não é verdade: O Alasca como parte dos Estados Unidos, Nakhchivan como parte do Azerbaijão e Kaliningrado como parte da Rússia não são contíguos. Como o território de um determinado país deve ser da mesma cor, quatro cores podem não ser suficientes. Por exemplo, considere um mapa simplificado, como o mostrado à esquerda: Neste mapa, as duas regiões rotuladas como A pertencem ao mesmo país, e devem ser da mesma cor. Este mapa então requer cinco cores, já que as duas regiões A juntas são contíguas a quatro outras regiões, cada uma delas contígua a todas as outras. Se A tivesse apenas três regiões, seis ou mais cores poderiam ser necessárias. Desta forma, é possível fazer mapas que precisam de um número arbitrariamente alto de cores. Uma construção semelhante também se aplica se uma única cor for usada para todas as massas de água, como é usual em mapas reais.
Uma versão mais fácil de afirmar do teorema utiliza a teoria dos gráficos. O conjunto de regiões de um mapa pode ser representado mais abstratamente como um gráfico não direcionado que tem um vértice para cada região e uma borda para cada par de regiões que compartilham um segmento de fronteira. Este gráfico é plano: ele pode ser desenhado no plano sem travessias, colocando cada vértice em um local arbitrariamente escolhido dentro da região a que corresponde, e desenhando as bordas como curvas que levam sem travessias dentro de cada região desde o local do vértice até cada ponto de fronteira compartilhado da região. Ao contrário, qualquer gráfico planar pode ser formado a partir de um mapa desta forma. Na terminologia teórica do gráfico, o teorema de quatro cores afirma que os vértices de cada gráfico planar podem ser coloridos com no máximo quatro cores para que não haja dois vértices adjacentes com a mesma cor, ou seja, "cada gráfico planar é quadricolor" (Thomas 1998, p. 849; Wilson 2002).

Exemplo de um mapa do Azerbaijão com regiões não contíguas

Este mapa não pode ser colorido com quatro cores
História
A primeira pessoa a mencionar o problema foi Francis Guthrie, em 1852. Ele era um estudante de direito na Inglaterra, na época. Ele descobriu que precisava de pelo menos quatro cores para colorir um mapa dos condados da Inglaterra. Augustus de Morgan discutiu o problema pela primeira vez, em uma carta que escreveu a Rowan Hamliton, em agosto de 1852. Na carta, de Morgan pergunta se quatro cores são realmente suficientes para colorir um mapa, de modo que os países que estão próximos uns dos outros tenham cores diferentes.
O matemático inglês Arthur Cayley apresentou o problema à sociedade matemática em Londres, em 1878. Em um ano, Alfred Kempe encontrou o que parecia ser uma prova do problema. Onze anos mais tarde, em 1890, Percy Heawood mostrou que a prova de Alfred estava errada. Peter Guthrie Tait apresentou outra tentativa de uma prova em 1880. Levou onze anos para mostrar que a prova de Tait também não funcionava. Em 1891, Julius Petersen pôde mostrar isso. Quando ele falsificou a prova de Cayley, Kempe também mostrou uma prova de um problema que ele chamou de teorema de Cinco Cor. O teorema diz que qualquer mapa desse tipo pode ser colorido com não mais do que cinco cores. Há duas restrições: Primeiro, qualquer país é contíguo, não há exclaves. A segunda restrição é que os países precisam ter uma fronteira comum; se eles só tocarem em um ponto, podem ser coloridos com a mesma cor. Mesmo que a prova de Kempe estivesse errada, ele usou algumas das idéias que mais tarde permitiriam uma prova correta.
Nas décadas de 1960 e 1970, Heinrich Heesch desenvolveu um primeiro esboço de uma prova por computador. Kenneth Appel e Wolfgang Haken melhoraram este esboço em 1976 (Robertson et al. 1996). Eles foram capazes de reduzir o número de casos que precisariam ser testados até 1936; uma versão posterior foi feita com base em testes de apenas 1476 casos. Cada caso precisava ser testado por um computador (Appel & Haken 1977).
Em 1996, Neil Robertson, Daniel Sanders, Paul Seymour e Robin Thomas melhoraram o método e reduziram o número de casos a serem testados para 663. Mais uma vez, cada caso precisava ser testado por computador.
Em 2005, Georges Gonthier e Benjamin Werner desenvolveram uma prova formal. Esta foi uma melhoria, pois permitiu utilizar pela primeira vez um software de comprovação de teorema. O software utilizado é chamado Coq.
O teorema de quatro cores é o primeiro grande problema matemático que foi provado com a ajuda de um computador. Como a prova não pode ser feita por um humano, alguns matemáticos não a reconheceram como correta. Para verificar a prova, é necessário confiar em um software e hardware que funcione corretamente para validar a prova. Como a prova foi feita por computador, ela também não é muito elegante.
Tentativas que se revelaram erradas
O teorema das quatro cores tem sido notório por ter atraído um grande número de provas falsas e provas falsas em sua longa história. No início, o The New York Times recusou-se a relatar a prova Appel-Haken. O jornal fez isso como uma questão de política; temia que a prova fosse mostrada falsa como as anteriores (Wilson 2002, p. 209). Algumas provas demoraram muito tempo, até que pudessem ser falsificadas: Para as provas de Kempe e Tait, falsificá-las demorou mais de uma década.
Os contra-exemplos mais simples geralmente tentam criar uma região que toca todas as outras. Isto força as demais regiões a serem coloridas com apenas três cores. Como o teorema das quatro cores é verdadeiro, isto é sempre possível; entretanto, como a pessoa que desenha o mapa está concentrada em uma grande região, ela não percebe que as regiões restantes podem, de fato, ser coloridas com três cores.
Este truque pode ser generalizado: Se as cores de algumas regiões em um mapa são escolhidas de antemão, torna-se impossível colorir as regiões restantes de tal forma que no total, apenas quatro cores são usadas. Alguém verificando o contra-exemplo pode pensar que não será necessário mudar a cor dessas regiões. Isto fará com que o contra-exemplo pareça válido, mesmo que não o seja.
Talvez um efeito subjacente a este equívoco comum seja o fato de que a restrição de cor não é transitória: uma região só tem que ser colorida de forma diferente das regiões que toca diretamente, não as regiões que tocam regiões que tocam. Se esta fosse a restrição, os gráficos planares exigiriam arbitrariamente um grande número de cores.
Outras falsas provas violam as suposições do teorema de formas inesperadas, como o uso de uma região que tem várias partes desconectadas, ou não permitir que regiões da mesma cor se toquem em um ponto.
Colorir mapas políticos
Na vida real, muitos países possuem exclaves ou colônias. Como eles pertencem ao país, eles precisam ser coloridos com a mesma cor do país de origem. Isto significa que normalmente são necessárias mais de quatro cores para colorir um tal mapa. Quando os matemáticos falam sobre o gráfico associado ao problema, eles dizem que isso não é planar. Mesmo que seja fácil verificar se um gráfico é plano, é muito difícil encontrar o menor número de cores necessárias para colori-lo. É NP-complete, que é um dos problemas mais difíceis que existem. O menor número de cores necessárias para colorir um gráfico é conhecido como seu número cromático. Muitos dos problemas que acontecem quando se tenta resolver o teorema das quatro cores estão relacionados com a matemática discreta. Por esta razão, métodos da topologia algébrica são freqüentemente utilizados.
Extensão para mapas "não planos".
O teorema de quatro cores exige que o "mapa" esteja sobre uma superfície plana, o que os matemáticos chamam de plano. Em 1890, Percy John Heawood criou o que hoje é chamado de conjectura Heawood: Ela faz a mesma pergunta que o teorema das quatro cores, mas para qualquer objeto topológico. Como exemplo, um toro pode ser colorido com, no máximo, sete cores. A conjectura de Heawood dá uma fórmula que funciona para todos esses objetos, exceto a garrafa de Klein.
Perguntas e Respostas
P: Qual é o teorema das quatro cores?
R: O teorema das quatro cores é um teorema matemático que diz que em qualquer superfície plana com regiões, as regiões podem ser coloridas com não mais do que quatro cores. As regiões adjacentes não devem ter a mesma cor.
P: Como foi estabelecida a primeira prova do teorema das quatro cores?
R: A primeira prova do teorema das quatro cores foi uma prova por exaustão, com 1.936 casos. Isso significa que ela foi estabelecida dividindo-a em casos e provando cada um separadamente.
P: Os cartógrafos estão interessados neste problema?
R: Não, os cartógrafos não estão muito interessados nesse problema, pois os mapas que utilizam apenas quatro cores são raros e geralmente exigem apenas três cores. Os livros sobre cartografia e história da elaboração de mapas não mencionam a propriedade de quatro cores.
P: O que é o teorema das cinco cores?
R: O teorema das cinco cores diz que cinco cores são suficientes para colorir um mapa e tem uma prova curta e elementar que foi provada no final do século 19.
P: Quão difícil foi provar que apenas quatro cores eram necessárias para colorir mapas?
R: Provar que apenas 4 cores eram necessárias para colorir mapas se revelou muito mais difícil do que se esperava, pois muitas provas falsas e falsos contra-exemplos apareceram desde sua primeira declaração em 1852.
P: Há algum exemplo de mapa onde 5 ou mais cores seriam necessárias para colorir corretamente todas as regiões?
R: Sim, um desses exemplos é quando uma região está rodeada por um número ímpar de outras que se tocam umas às outras num ciclo - 5 ou mais cores podem ser necessárias para colorir corretamente todas as regiões neste caso.
Pesquise na enciclopédia

