Trigonometria

A trigonometria (do grego trigonon = três ângulos e metron = medida) é uma parte da matemática elementar que lida com ângulos, triângulos e funções trigonométricas tais como seno (pecado abreviado), cosseno (coseno abreviado) e tangente (bronzeado abreviado). Tem alguma conexão com a geometria, embora haja desacordo sobre exatamente o que é essa conexão; para alguns, a trigonometria é apenas uma seção da geometria.

Visão geral e definições

A trigonometria usa um grande número de palavras específicas para descrever partes de um triângulo. Algumas das definições em trigonometria são:

Triângulo em ângulo reto - Um triângulo em ângulo reto é um triângulo que tem um ângulo igual a 90 graus. (Um triângulo não pode ter mais de um ângulo reto) As proporções trigonométricas padrão só podem ser usadas em triângulos retos.
Hipotenusa - A hipotenusa de um triângulo é o lado mais longo, e o lado oposto ao ângulo reto. Por exemplo, para o triângulo da direita, a hipotenusa é o lado c.
Oposto de um ângulo - O lado oposto de um ângulo é o lado que não se intercepta com o vértice do ângulo. Por exemplo, o lado a é o oposto do ângulo A no triângulo à direita.
Adjacente de um ângulo - O lado adjacente de um ângulo é o lado que intercepta o vértice do ângulo, mas não é a hipotenusa. Por exemplo, o lado b é adjacente ao ângulo A no triângulo à direita.

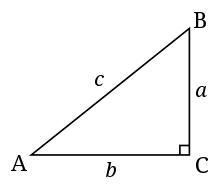
Um triângulo padrão à direita. C é o ângulo reto nesta foto

Índices trigonométricos

Há três razões trigonométricas principais para os triângulos retos, e três recíprocas dessas razões. Há 6 relações totais. Elas são:

Seno (pecado) - O seno de um ângulo é igual ao da Hipotenusa oposta ao estilo de um jogo (Opposite) \sobre o texto (Hypotenuse}}}}) ${{\text{Opposite}} \over {\text{Hypotenuse}}}$
Coseno (cos) - O coseno de um ângulo é igual ao da Hipotenusa Adjacente (estilo de jogo). \sobre o texto (Hypotenuse}}}}) ${{\text{Adjacent}} \over {\text{Hypotenuse}}}$
Tangente (bronzeado) - A tangente de um ângulo é igual ao adjacente oposto ao estilo de um jogo \sobre o texto (Adacent}}}}) ${{\text{Opposite}} \over {\text{Adjacent}}}$

Os recíprocos destes rácios são:

Cosecant (csc) - O cosecant de um ângulo é igual ao Hypotenuse Opposite (estilo de exibição de texto Hypotenuse). \sobre o texto (Opposite}}}} ${{\text{Hypotenuse}} \over {\text{Opposite}}}$ ou csc θ = 1 pecado θ estilo de jogo csc = 1 no tetá $\csc \theta ={1 \over \sin \theta }$

Secant (seg) - A secant de um ângulo é igual à Hypotenuse Adjacent {{\i1}displaystyle {\i} \SOBRE o texto (Adjacent}}}} ${{\text{Hypotenuse}} \over {\text{Adjacent}}}$ ou seg θ = 1 cos θ $\sec \theta ={1 \over \cos \theta }$

Cotangent (berço) - O cotangent de um ângulo é igual ao adjacente ao estilo oposto ao do jogo. \sobre o texto (Opposite}}}} ${{\text{Adjacent}} \over {\text{Opposite}}}$ ou berço θ = 1 tan θ estilo de jogo = 1 téta = 1 téta $\cot \theta ={1 \over \tan \theta }$

Os estudantes frequentemente usam uma mnemônica para se lembrar desta relação. As proporções senoidal, co-seno e tangente em um triângulo direito podem ser lembradas representando-as como cordas de letras, tais como SOH-CAH-TOA:

Seno = Oposto ÷ Hipotenusa

Cosina = Adjacente ÷ Hipotenusa

Tangente = Oposto ÷ Adjacente

Usando trigonometria

Com os pecados e cossenos pode-se responder praticamente todas as perguntas sobre os triângulos. Isto é chamado de "resolver" o triângulo. Pode-se trabalhar os ângulos e lados restantes de qualquer triângulo assim que dois lados e seu ângulo incluído ou dois ângulos e um lado ou três lados forem conhecidos. Estas leis são úteis em todos os ramos da geometria, já que cada polígono pode ser descrito como uma combinação de triângulos.

A trigonometria também é vital na topografia, na análise vetorial e no estudo de funções periódicas.

Existe também a trigonometria esférica, que lida com a geometria esférica. Isto é usado para cálculos em astronomia, geodésia e navegação.

Leis de trigonometria

Lei de Sines

a Pecado A = b Pecado B = c Pecado C {{\i1}displaystyle {\i} \sobre o texto \sobre o texto (Tradução) \sobre o texto (em C}}}}) ${{\text{a}} \over {\text{Sin A}}}={{\text{b}} \over {\text{Sin B}}}={{\text{c}} \over {\text{Sin C}}}$

Lei de Cosines

a 2 = b 2 + c 2 - 2 b c cos ( A ) {\i1}=b^{2}=b^{2}+c^{2}-2bc^cos(A)} $a^{2}=b^{2}+c^{2}-2bc\cos(A)$

Lei de Tangentes

a - b a + b = bronzeado ( 1 2 ( A - B ) ) bronzeado ( 1 2 ( A + B ) ) estilo de jogo {\a+b}{a+b}}=frac {\a(1}(A-B)){tan(2}(A-B)){tan(1}(A+B) ${\frac {a-b}{a+b}}={\frac {\tan({\frac {1}{2}}(A-B))}{\tan({\frac {1}{2}}(A+B))}}$