Algoritmo

Comparação de algoritmos

Geralmente há mais de uma maneira de resolver um problema. Pode haver muitas receitas diferentes para fazer um determinado prato que parece diferente, mas acaba provando o mesmo quando tudo é dito e feito. O mesmo se aplica aos algoritmos. Entretanto, algumas dessas maneiras serão melhores do que outras. Se uma receita precisa de muitos ingredientes complicados que você não tem, ela não é tão boa quanto uma simples receita. Quando consideramos os algoritmos como uma forma de resolver problemas, muitas vezes queremos saber quanto tempo levaria um computador para resolver o problema usando um algoritmo específico. Quando escrevemos algoritmos, gostamos que nosso algoritmo leve o menor tempo possível para que possamos resolver nosso problema o mais rápido possível.

Na culinária, algumas receitas são mais difíceis de fazer do que outras, porque levam mais tempo para terminar ou têm mais coisas para manter o controle. O mesmo acontece com os algoritmos, e os algoritmos são melhores quando são mais fáceis de serem feitos pelo computador. A coisa que mede a dificuldade de um algoritmo é chamada complexidade. Quando perguntamos quão complexo é um algoritmo, muitas vezes queremos saber quanto tempo levará um computador para resolver o problema que queremos que ele resolva.

Ordenação

Este é um exemplo de algoritmo de classificação de cartões com cores em pilhas da mesma cor:

1. Pegue todas as cartas.
2. Pegue uma carta de sua mão e veja a cor da carta.
3. Se já houver uma pilha de cartas dessa cor, coloque esta carta nessa pilha.
4. Se não houver uma pilha de cartas dessa cor, faça uma nova pilha só com esta cor de cartão.
5. Se ainda houver um cartão em sua mão, volte para o segundo passo.
6. Se ainda não houver um cartão em sua mão, então os cartões são classificados. Você está feito.

Ordenação por números

Estes são exemplos de algoritmos para classificar uma pilha de cartões com muitos números diferentes, para que os números estejam em ordem.

Os jogadores começam com uma pilha de cartas que não foram classificadas.

Primeiro algoritmo

Este algoritmo passa pela pilha de cartas, uma carta de cada vez. Esta carta é comparada com a próxima carta na pilha. Observe que esta posição só muda no passo 6. Este algoritmo é chamado de bubble sort. Ele é lento.

1. Se a pilha de cartões estiver vazia, ou se ela contiver apenas um cartão, ela é classificada; você está acabado.
2. Pegue a pilha de cartas. Veja a primeira carta (a parte superior) da pilha.
3. O cartão que você está olhando é o cartão A. A posição onde o cartão A está atualmente, está na pilha P.
4. Se não houver mais cartas na pilha depois da carta A, vá para o passo 8.
5. A próxima carta na pilha é a carta B.
6. Se a carta B tiver um número inferior à carta A, troque as posições das cartas A e B. Lembre-se de que você fez isso. Quando trocar as cartas, não mude a posição P.
7. Se houver outra carta na pilha após a posição P, olhe para ela; volte ao passo 3.
8. Se você não trocou a posição de nenhuma carta na última rodada, você está feito; a pilha de cartas é classificada.
9. Caso contrário, volte ao passo 2.

Exemplo passo a passo

Vamos pegar uma pilha de cartões com os números "5 1 4 2 8", e classificá-la do menor número para o maior usando este algoritmo. Em cada etapa, o algoritmo compara os elementos escritos em negrito. A parte superior da pilha de cartas está do lado esquerdo.

Primeiro passe:
( 5 1 4 2 8 ) → {\a2}displaystyle {\a2} ( 1 5 4 2 8 ) Aqui, o algoritmo compara os dois primeiros elementos, e os troca.
( 1 5 4 2 8 ) → {\i1}a ( 1 4 5 2 8 )
( 1 4 5 2 8 ) → {\i1}displaystyle {\i} ( 1 4 2 5 8 )
( 1 4 2 5 8 ) → {\i1}displaystyle {\i} ( 1 4 2 5 8 ) Estes elementos já estão em ordem, portanto o algoritmo não os troca.
Segundo passe:
( 1 4 2 5 8 ) → {\i1}displaystyle {\i1} ( 1 4 2 5 8 )
( 1 4 2 5 8 ) → {\i1}displaystyle {\i} ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\i1}displaystyle {\i} ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\i1}displaystyle {\i} ( 1 2 4 5 8 )
Agora, a pilha de cartões já
 está classificada, mas nosso algoritmo não sabe disso. O algoritmo precisa de um passe inteiro sem nenhuma troca para saber que está classificado.
Terceiro passe:
( 1 2 4 5 8 ) → {\a10} ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\i1}displaystyle {\i} ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\i1}displaystyle {\i} ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\i1}displaystyle {\i} ( 1 2 4 5 8 )
Finalmente, a matriz é classificada, e o algoritmo pode parar.

História

Este é um algoritmo fácil de entender para a classificação. Os cientistas da computação o chamaram de Bubble sort, porque elementos menores subirão ao topo, mudando sua posição em cada corrida. Infelizmente, o algoritmo não é muito bom, porque precisa de muito tempo (muitos passam pela pilha de cartas) para classificá-lo.

Segundo algoritmo

Este algoritmo usa outra idéia. Às vezes a solução de um problema é difícil, mas o problema pode ser alterado para que seja feito de problemas mais simples que sejam mais fáceis de resolver. Isto é chamado de recursividade. É mais difícil de entender do que o primeiro exemplo, mas ele dará um algoritmo melhor.

Idéia básica

1. Se a pilha não tiver cartões, ou tiver apenas um cartão, ela é classificada, e você está acabado.
2. Dividir a pilha de cartas em duas metades de aproximadamente o mesmo tamanho. Se houver um número ímpar de cartas, uma das duas pilhas terá uma carta a mais do que a outra.
3. Ordene cada uma das duas pilhas usando este algoritmo (Para cada pilha, comece no item 1 desta lista).
4. Fundir as duas pilhas classificadas, como descrito abaixo.
5. O resultado é uma pilha classificada de cartas. Você está feito.

Fusão de duas pilhas

Isto funciona com duas pilhas de cartões. Uma delas é chamada de A, a outra de B. Há uma terceira pilha que está vazia no início, chamada de C. No final, ela conterá o resultado.

1. Se a pilha A ou a pilha B estiver vazia, coloque todas as cartas da pilha que não está vazia em cima da pilha C; você está feito, a pilha C é o resultado da fusão. (Nota: pegue a pilha inteira, e coloque-a na pilha C; fazê-lo cartão por cartão mudará a ordem e não funcionará como deveria).
2. Veja as cartas superiores da pilha A e da pilha B. Coloque a que tem o número inferior em cima da pilha C. Se a pilha C não tinha cartas nela, ela terá agora uma carta.
3. Se a pilha A ou a pilha B ainda tiver cartões, volte ao passo 1 para classificá-los.

História

John von Neumann desenvolveu este algoritmo em 1945. Ele não o chamou de Sorting by numbers, ele o chamou de Mergesort. É um algoritmo muito bom para ordenação, comparado a outros.

Terceiro algoritmo

O primeiro algoritmo leva muito mais tempo para classificar as cartas do que o segundo, mas pode ser melhorado (melhorado). Olhando para a classificação de bolhas, pode-se notar que as cartas com números altos se movem do topo da pilha muito rapidamente, mas as cartas com números baixos na parte inferior da pilha levam muito tempo para subir (mover-se para o topo). Para melhorar o primeiro algoritmo aqui é a idéia:

Ao invés de comparar duas cartas que estão ao lado uma da outra, no início é escolhida uma carta "especial". Todas as outras cartas são então comparadas com esta carta.

1. Começamos com uma pilha A. Haverá duas outras pilhas B e C, que serão criadas mais tarde.
2. Se a pilha A não tem cartões, ou tem apenas um cartão, terminamos a triagem.
3. Uma carta é retirada da pilha A, se possível de forma aleatória. Isto é chamado de pivô.
4. Todas as cartas restantes da pilha A são comparadas a este pivô. As cartas com um número menor vão para a pilha B, aquelas com um número igual ou maior vão para a pilha C.
5. Se houver algum cartão nas pilhas B ou C, estas pilhas precisam ser classificadas com o mesmo algoritmo (Comece na pos 1 desta lista para a pilha B e para a pilha C, por sua vez).
6. Feito. A pilha classificada de cartas tem primeiro a pilha classificada B, depois o pivô, e depois a pilha classificada C.

História

Este algoritmo foi desenvolvido por C. A. R. Hoare em 1960. É um dos algoritmos mais utilizados hoje em dia para a classificação. Ele é chamado de Quicksort.

Animação que mostra como funciona um tipo de bolha


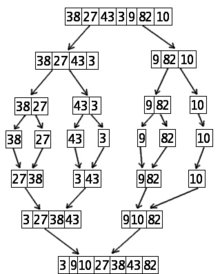
Ordenação de 7 números usando o segundo algoritmo de Ordenação por números (Mergesort)


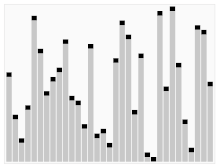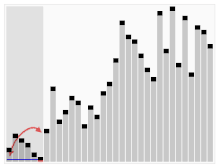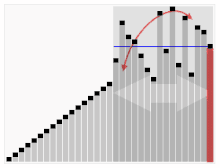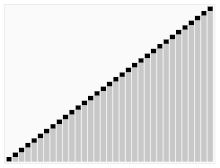
O terceiro algoritmo para a classificação de cartões. O elemento com a barra vermelha é escolhido como o pivô. No início, é o elemento todo à direita. Este algoritmo é chamado de Quicksort.

Colocando algoritmos juntos

Se os jogadores tiverem cartas com cores e números, eles podem classificá-las por cor e número se fizerem o algoritmo de "classificação por cores", então façam o algoritmo de "classificação por números" para cada pilha colorida, então juntem as pilhas.

Os algoritmos de ordenação por números são mais difíceis de fazer do que o algoritmo de ordenação por cores, porque eles podem ter que fazer os passos novamente muitas vezes. Pode-se dizer que a ordenação por números é mais complexa.

Páginas relacionadas

• O algoritmo euclidiano foi encontrado há mais de 2000 anos. Ele é capaz de encontrar o maior divisor comum de dois números.