Função (matemática)
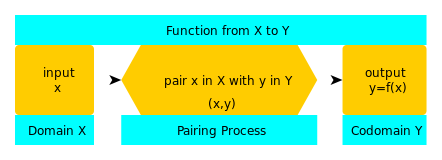
Em matemática, uma função é um objecto matemático que produz uma saída, quando dada uma entrada - pode ser um número, um vector, ou qualquer coisa que possa existir dentro de um conjunto de coisas.
Assim, uma função é como uma máquina, que toma valores de x e devolve uma saída y. O conjunto de todos os valores que x pode ter é chamado de domínio. O conjunto que contém todos os valores que y pode ter é chamado de codomínio.
Se isto acontecer, dizemos que y é uma função de x, e escrevemos y =f(x). f é o nome da função e escreve-se f : X → Y {\displaystyle f:X\to Y} 
(função de X a Y) para representar as três partes da função: o domínio (x), o codomínio (y) e o processo de emparelhamento (a seta).
Um exemplo de uma função é f(x)=x+1 Um dá um número natural x 
(0,1,2,3...) como entrada e recebe um número natural y (0,1,2,3...) como entrada e recebe um número natural y (0,1,2,3...) como entrada 
A ideia de uma função foi criada para cobrir todo o tipo de possibilidades. A função não tem de ser uma equação. A ideia principal é que as entradas e saídas são emparelhadas de alguma forma, mesmo que o processo seja muito complicado.
Metáforas
Tabelas
As entradas e saídas podem ser colocadas numa tabela como a imagem; isto é fácil se não houver demasiados dados.
Gráficos
Na imagem pode ver-se que tanto 2 como 3 foram emparelhados com c; isto não é permitido na outra direcção, 2 não puderam sair c e d,cada entrada só pode ter uma saída. Todos os f ( x ) f(x)}displaystyle f(x)} 
(c e d na imagem) são normalmente chamados o conjunto de imagens de f {\displaystyle f}
e o conjunto de imagens pode ser todo o codomínio ou não. Pode-se dizer que o subconjunto A do codomínio com o conjunto de imagens é f(A). Se as entradas e saídas tiverem uma ordem, é fácil traçá-las num gráfico: 
Desta forma, a imagem vem na imagem do conjunto A. Isto fará com que 2 e 3 tenham emparelhado com não seja permitido na outra direcção, mesmo que se possa fazer entre codomínio ou não. Pode concluir-se que o subconjunto A do codomínio é o conjunto da imagem é F(A).
História
Nos anos 1690, GottfriedLeibniz e Johann Bernoulli usaram a função da palavra em letras entre eles, pelo que o conceito moderno começou ao mesmo tempo que o cálculo.
Em 1748 Leonhard Euler deu: "Uma função de uma quantidade variável é uma expressão analítica composta de qualquer forma da quantidade variável e números ou quantidades constantes" e depois, em 1755: "Se algumas quantidades dependem assim de outras quantidades que, se as últimas forem alteradas, as primeiras sofrem alterações, então as primeiras quantidades são chamadas funções das segundas. Esta definição aplica-se bastante amplamente e inclui todas as formas em que uma quantidade pode ser determinada por outra. Se, portanto, x denota uma quantidade variável, então todas as quantidades que dependem de x de qualquer forma, ou são determinadas por ela, são chamadas funções de x." que é muito moderna.
Normalmente, o Dirichlet é creditado com a versão utilizada nas escolas até à segunda metade do século XX: "y é uma função de uma variável x, definida no intervalo a < x < b, se a cada valor da variável x neste intervalo corresponde um valor definido da variável y. Além disso, é irrelevante a forma como esta correspondência é estabelecida".
Em 1939, o Bourbaki generalizou a definição de Dirichlet e deu uma versão teórica da definição como uma correspondência entre entradas e saídas; isto foi utilizado nas escolas a partir de cerca de 1960.
Finalmente, em 1970, o Bourbaki deu a definição moderna como um triplo f = ( X , Y , F ) f=(X,Y,F)} 
, com F ⊂ X × Y , ( x , f ( x ) ) ∈ F {\i1}f {\i1}subset ao estilo F {\i1}subset X vezes Y,(x,f(x))in F}
(i.e. f : X → Y {\i1}displaystyle f:X\i} and F = { ( x , f ( x ) ) | x ∈ X , f ( x ) ∈ Y } F={{(x,f(x))|x em X,f(x)} em Y} 
).
Tipos de funções
- Funções elementares - As funções que são geralmente estudadas na escola: fracções, raízes quadradas, as funções seno, cosseno e tangente e algumas outras funções.
- Funções não elementares - a maioria delas não utiliza operações que não aprendemos na escola (como + ou -, ou poderes). Muitos integrais são não-elementares.
- Funções inversas - Funções que desfazem outra função. Por exemplo: se F(x) é o inverso de f(x)=y, então F(y)=x. Nem todas as funções têm inversos.
- Funções especiais: Funções que têm nomes. Por exemplo: seno, co-seno e tangente. Funções como f(x)=3x (três vezes x) não são chamadas funções especiais. Podem ser elementares, não elementares ou inversas.
Perguntas e Respostas
P: O que é uma função na matemática?
R: Uma função em matemática é um objeto que produz uma saída quando recebe uma entrada, que pode ser um número, um vetor ou qualquer coisa que possa existir dentro de um conjunto de coisas.
P: O que são os dois conjuntos associados a funções?
R: O conjunto de todos os valores que x pode ter é chamado de domínio e o conjunto que contém todos os valores que y pode ter é chamado de codomínio.
P: Como as funções são freqüentemente designadas?
R: As funções são freqüentemente indicadas por letras itálicas como f, g, h.
P: Como representamos uma função?
R: Representamos uma função escrevendo y = f(x), onde f é o nome da função e se escreve f : X → Y (função de X a Y) para representar as três partes da função - domínio (X), codomínio (Y) e processo de emparelhamento (a seta).
P: O senhor pode dar um exemplo de uma função?
R: Um exemplo de uma função é f(x) = x + 1. Um dá um número natural x como entrada e recebe um número natural y que é x + 1. Por exemplo, dar 3 como entrada para f resulta em uma saída de 4.
P: Toda função precisa ser uma equação?
R: Não, nem todas as funções precisam ser uma equação. A idéia principal por trás das funções é que as entradas e saídas são emparelhadas de alguma maneira - mesmo que isso possa ser muito complicado.
