Vetor

Exemplos de vetores

• John caminha para o norte 20 metros. A direção "norte" junto com a distância "20 metros" é um vetor.
• Uma maçã cai a 10 metros por segundo. A direção "para baixo" combinada com a velocidade "10 metros por segundo" é um vetor. Este tipo de vetor também é chamado de velocidade.

Exemplos de escalares

• A distância entre dois lugares é de 10 quilômetros. Esta distância não é um vetor porque não contém uma direção.
• O número de frutas em uma caixa não é um vetor.
• Uma pessoa apontando não é um vetor porque existe apenas uma direção. Não há nenhuma magnitude (a distância do dedo da pessoa a um edifício, por exemplo).
• O comprimento de um objeto.
• Um carro dirige a 100 quilômetros por hora. Isto não descreve um vetor, pois existe apenas uma magnitude, mas nenhuma direção.

Mais exemplos de vetores

• O deslocamento é um vetor. Deslocamento é a distância que algo se move em uma determinada direção. Uma medida de distância sozinha é um escalar.
• A força que inclui a direção é um vetor.
• A velocidade é um vetor, porque é uma velocidade em uma determinada direção.
• Aceleração é a taxa de mudança de velocidade. Um objeto está acelerando se estiver mudando de velocidade ou mudando de direção.

Como adicionar vetores

Adicionando vetores no papel usando o método da cabeça à cauda

O método Head to Tail de adição de vetores é útil para fazer uma estimativa no papel do resultado da adição de dois vetores. Para fazer isso:

• Cada vetor é desenhado como uma seta com uma quantidade de comprimento atrás dele, onde cada unidade de comprimento no papel representa uma certa magnitude do vetor.
• Desenhe o próximo vetor, com a cauda (final) do segundo vetor na cabeça (frente) do primeiro vetor.
• Repetir para todos os outros vetores: Desenhe a cauda do próximo vetor à frente do anterior.
• Traçar uma linha desde a cauda do primeiro vetor até a cabeça do último vetor - isso é a resultante (soma) de todos os vetores.

É chamado de método "Cabeça para Cauda", porque cada cabeça do vetor anterior leva à cauda da próxima.

Usando o formulário de componentes

^{[precisa ser explicado]}

Usar o formulário de componentes para adicionar dois vetores significa literalmente adicionar os componentes dos vetores para criar um novo vetor. Por exemplo, deixe a e b serem dois vetores bidimensionais. Esses vetores podem ser escritos em termos de seus componentes.

a = ( a x , a y ) {\a} {a} =(a_{x},a_{y})}

b = ( b x , b y ) {\i} {b} =(b_{x},b_{y})}

Suponha que c é a soma desses dois vetores, de modo que c = a + b. Isto significa que c = ( a x + b x , a y + b y ) {\i1}mathbf {c} =(a_{x}+b_{x},a_{y}+b_{y})} .

Aqui está um exemplo de adição de dois vetores, utilizando suas formas componentes.

a = ( 3 , - 1 ) {\an8} {a} =(3,-1)}

b = ( 2 , 2 ) {\i1}displaystyle \i}mathbf {b} =(2,2)}

c = a + b {\i1}mathbf {c} =mathbf {a} +{\i1}mathbf {b} }

= ( a x + b x , a y + b y ) {\i1}displaystyle =(a_{x}+b_{x},a_{y}+b_{y})}

= ( 3 + 2 , - 1 + 2 ) {\i1}displaystyle =(3+2,-1+2)}

= ( 5 , 1 ) {\i1}displaystyle =(5,1)}

Este método funciona para todos os vetores, não apenas para os bidimensionais.

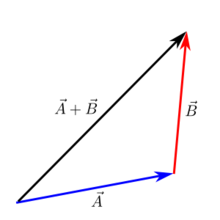
Adição "cabeça a cabeça

Como multiplicar os vetores

Usando o produto ponto

O produto ponto é um método para multiplicar os vetores. Ele produz um escalar. Ele utiliza a forma de componentes:

a = ( 2 , 3 ) b = ( 1 , 4 ) a ⋅ b = ( 2 , 3 ) ⋅ ( 1 , 4 ) = ( 2 ⋅ 1 ) + ( 3 ⋅ 4 ) = 2 + 12 = 14 {\i1}mathbf {a} =(2,3)mathbf {b} =(1,4)mathbf {a} {cdot {b} =(2,3){cdot (1,4){2){cdot 1)+(3)cdot 4){a}=2+12=14end{alinhado

Usando o produto cruzado

O produto cruzado é outro método para multiplicar os vetores. Ele produz outro vetor. Usando a forma de componentes:

a × b = | a | b | sin ( θ ) n {\i1}displaystyle {a}mathbf {a} times |mathbf {b} =|mathbf {a} ||mathbf {b} |\em (theta )mathbf {n} }

Aqui um estilo de exibição |Significa o comprimento de um jogo ao estilo de uma peça de teatro. e n estilo de jogo de matemática. é o vetor da unidade em ângulos retos a ambos os ângulos, ao estilo de um e b b estilo de jogo de jogo de matemática } .

Multiplicando por um escalar

Para multiplicar um vetor por um escalar (um número normal), multiplica-se o número por cada componente do vetor:

c x = ( c x 1 , c x 2 , . . . , c x n ) {\i1}displaystyle c\i}, mathbf {x} =(c\i, x_{1},c\i, x_{2},...,c\i, x_{n})}

Um exemplo disso é

c = 5 x = ( 3 , 4 ) c x = ( 5 ⋅ 3 , 5 ⋅ 4 ) = ( 15 , 20 ) {\i1}displaystyle {\i1}c=5mathbf {x} =(3,4){\i},{\i}mathbf {x} =(5\i3,5){\i} {\i1}(15,20){\i}end{\i1}end{\i}}alinhado

Páginas relacionadas

• Gráficos vetoriais
• Campo vetorial