Álgebra

Álgebra (do árabe: الجبر, transliterado "al-jabr", que significa "reunião de partes quebradas") é uma parte da matemática (muitas vezes chamada matemática nos Estados Unidos e matemática ou numeracia no Reino Unido). Ela usa variáveis para representar um valor que ainda não é conhecido. Quando um sinal de igual (=) é usado, isto é chamado de equação. Uma equação muito simples usando uma variável é: 2 + 3 = x. Neste exemplo, x = 5, ou também poderia ser dito que "x é igual a cinco". Isto é chamado de solução para x.

Além das equações, existem desigualdades (menores e maiores do que). Um tipo especial de equação é chamado de função. Ela é freqüentemente usada na criação de gráficos porque sempre transforma uma entrada em uma saída.

A álgebra pode ser usada para resolver problemas reais porque as regras de trabalho da álgebra na vida real e os números podem ser usados para representar os valores das coisas reais. A física, a engenharia e a programação de computadores são áreas que usam álgebra o tempo todo. Também é útil conhecer em topografia, construção e negócios, especialmente em contabilidade.

As pessoas que fazem álgebra utilizam as regras de números e operações matemáticas utilizadas em números. As mais simples são adicionar, subtrair, multiplicar e dividir. As operações mais avançadas envolvem expoentes, começando com quadrados e raízes quadradas.

A álgebra foi usada pela primeira vez para resolver equações e desigualdades. Dois exemplos são as equações lineares (a equação de uma linha reta, y=mx+b) e as equações quadráticas, que têm variáveis que são quadradas (multiplicadas por si mesmas, por exemplo: 2*2, 3*3, ou x*x).

História

As primeiras formas de álgebra foram desenvolvidas pelos babilônios e pelos geômetros gregos, como o Herói de Alexandria. Entretanto, a palavra "álgebra" é uma forma latina da palavra árabe Al-Jabr ("casting") e vem de um livro de matemática Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah, ("Essay on the Computation of Casting and Equation") escrito no século IX por um matemático persa, Muhammad ibn Mūsā al-Khwārizmī, que era um muçulmano nascido em Khwarizm no Uzbequistão. Ele floresceu sob o domínio de Al-Ma'moun em Bagdá, Iraque até 813-833 d.C., e morreu por volta de 840 d.C. O livro foi trazido para a Europa e traduzido para o latim no século XII. O livro recebeu então o nome de 'Álgebra'. (O final do nome do matemático, al-Khwarizmi, foi mudado para uma palavra mais fácil de dizer em latim, e tornou-se o algoritmo da palavra inglesa).

Exemplos

Aqui está um exemplo simples de um problema de álgebra:

Sue tem 12 balas, e Ann tem 24 balas. Eles decidem compartilhar para que tenham o mesmo número de balas. Quantos balas cada um terá?

Estes são os passos que você pode usar para resolver o problema:

Para ter o mesmo número de balas, Ann tem que dar algumas para a Sue. Deixe x representar o número de balas que Ann dá à Sue.
Os doces de Sue, mais x, devem ser os mesmos que os doces de Ann menos x. Isto está escrito como: 12 + x = 24 - x
Subtrair 12 de ambos os lados da equação. Isto dá: x = 12 - x. (O que acontece em um lado do sinal de igual deve acontecer no outro lado também, para que a equação ainda seja verdadeira. Assim, neste caso, quando 12 foi subtraído de ambos os lados, houve um passo médio de 12 + x - 12 = 24 - x - 12. Depois que uma pessoa se sente confortável com isto, o passo do meio não é anotado).
Acrescente x a ambos os lados da equação. Isto dá: 2x = 12
Dividir ambos os lados da equação por 2. Isto dá x = 6. A resposta é seis. Se Ann der à Sue 6 balas, elas terão o mesmo número de balas.
Para verificar isso, coloque 6 de volta na equação original onde x estava: 12 + 6 = 24 - 6
Isto dá 18=18, o que é verdade. Cada um deles agora tem 18 balas.

Com a prática, a álgebra pode ser usada quando confrontada com um problema que é muito difícil de resolver de qualquer outra forma. Problemas como construir uma auto-estrada, projetar um telefone celular ou encontrar a cura para uma doença, todos requerem álgebra.

Álgebra de escrita

Como na maioria das partes da matemática, adicionar z a y (ou y mais z) é escrito como y + z. Subtrair z de y (ou y menos z) é escrito como y - z. Dividir y por z (ou y sobre z: y z {\displaystyle y \displaystyle y \dover z} ${y \over z}$ ) é escrito como y ÷ z ou y/z. y/z é mais comumente usado.

Em álgebra, multiplicar y por z (ou y vezes z) pode ser escrito de 4 maneiras: y × z, y * z, y-z, ou apenas yz. O símbolo de multiplicação "×" geralmente não é usado, porque se parece demais com a letra x, que é freqüentemente usada como uma variável. Também, ao multiplicar uma expressão maior, podem ser usados parênteses: y (z+1).

Quando multiplicamos um número e uma letra em álgebra, escrevemos o número na frente da letra: 5 × y = 5y. Quando o número é 1, então o 1 não é escrito porque 1 vezes qualquer número é esse número (1 × y = y) e, portanto, não é necessário.

Como nota lateral, você não precisa usar as letras x ou y em álgebra. As variáveis são apenas símbolos que significam algum número ou valor desconhecido, por isso você pode usar qualquer variável. x e y são as mais comuns, no entanto.

Funções e gráficos

Uma parte importante da álgebra é o estudo das funções, uma vez que as funções freqüentemente aparecem em equações que estamos tentando resolver. Uma função é como uma máquina na qual você pode colocar um número (ou números) e obter um certo número (ou números). Ao utilizar funções, os gráficos podem ser ferramentas poderosas para nos ajudar a estudar as soluções para as equações.

Um gráfico é uma figura que mostra todos os valores das variáveis que tornam a equação ou desigualdade verdadeira. Normalmente isto é fácil de fazer quando há apenas uma ou duas variáveis. O gráfico é freqüentemente uma linha, e se a linha não dobra ou vai diretamente para cima e para baixo pode ser descrita pela fórmula básica y = mx + b. A variável b é o y-intercepção do gráfico (onde a linha cruza o eixo vertical) e m é a inclinação ou declive da linha. Esta fórmula se aplica às coordenadas de um gráfico, onde cada ponto da linha é escrito (x, y).

Em alguns problemas matemáticos como a equação de uma linha, pode haver mais de uma variável (x e y neste caso). Para encontrar pontos na linha, uma variável é alterada. A variável que é alterada é chamada de variável "independente". Em seguida, a matemática é feita para fazer um número. O número que é feito é chamado de variável "dependente". Na maioria das vezes, a variável independente é escrita como x e a variável dependente é escrita como y, por exemplo, em y = 3x + 1. Isto é freqüentemente colocado em um gráfico, usando um eixo x (indo para a esquerda e direita) e um eixo y (indo para cima e para baixo). Também pode ser escrita em forma de função: f(x) = 3x + 1. Assim, neste exemplo, poderíamos colocar 5 para x e obter y = 16. Colocando em 2 para x, obteríamos y=7. E 0 por x obteria y=1. Assim, haveria uma linha passando pelos pontos (5,16), (2,7) e (0,1), como visto no gráfico à direita.

Se x tem uma potência de 1, é uma linha reta. Se for quadrado ou alguma outra potência, será curvado. Se ele usa uma desigualdade (< ou > ), então geralmente parte do gráfico é sombreada, seja acima ou abaixo da linha.

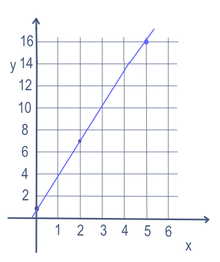
Equação linear para y=3x+1

Regras de álgebra

Na álgebra, há algumas regras que podem ser usadas para uma melhor compreensão das equações. Estas são chamadas de regras de álgebra. Embora estas regras possam parecer sem sentido ou óbvias, é sábio entender que estas propriedades não se sustentam em todos os ramos da matemática. Portanto, será útil saber como estas regras axiomáticas são declaradas, antes de tomá-las como garantidas. Antes de prosseguir com as regras, reflita sobre duas definições que serão dadas.

O oposto - o oposto de um estilo de exibição a é - um estilo de exibição -a .
Reciprocidade - a reciprocidade de um estilo de jogo a é 1 um estilo de jogo frac 1 ${\frac {1}{a}}$ .

Regras

Propriedade comutativa de adição

Comutativo" significa que uma função tem o mesmo resultado se os números forem trocados. Em outras palavras, a ordem dos termos em uma equação não importa. Quando o operador de dois termos é uma adição, a 'propriedade comutativa da adição' é aplicável. Em termos algébricos, isto dá a + b = b + a {\\i1 a+b=b+a} a+b=b+a .

Note que isto não se aplica à subtração! (isto é, a - b ≠ b - a {\i1}a {\i1}displaystyle a-b-b\neq b-a} $a-b\neq b-a$ )

Propriedade comutativa da multiplicação

Quando o operador de dois termos é uma multiplicação, a "propriedade comutativa da multiplicação" é aplicável. Em termos algébricos, isto dá um ⋅ b = b ⋅ a {\i1}displaystyle a\i}cdot b=b\cdot a} $a\cdot b=b\cdot a$ .

Note que isto não se aplica à divisão! (i.e. a b ≠ b a {\i1}displaystyle {\i}{a}{b}neq {\i}frac {b}{a}} ${\frac {a}{b}}\neq {\frac {b}{a}}$ a ≠ b b b b $a\neq b$ )

Propriedade associativa de adição

Associativo" refere-se ao agrupamento de números. A propriedade associativa de adição implica que, ao adicionar três ou mais termos, não importa como esses termos são agrupados. Algebraicamente, isto dá a + ( b + c ) = ( a + b ) + c {\\i1} estilo de jogo a+(b+c)=(a+b)+c} . Note que isto não é válido para subtração, por exemplo, 1 = 0 - ( 0 - 1 ) ≠ ( 0 - 0 ) - 1 = - 1 {\displaystyle 1=0-(0-1)\neq (0-0)-1=-1} $1=0-(0-1)\neq (0-0)-1=-1$ (ver a propriedade distributiva).

Propriedade associativa de multiplicação

A propriedade associativa da multiplicação implica que, ao multiplicar três ou mais termos, não importa como esses termos são agrupados. Algebraicamente, isto dá um ⋅ ( b ⋅ c ) = ( a ⋅ b ) ⋅ c {\i1}displaystyle a\i}cdot (b\cdot c)=(a\i}cdot b)cdot c} $a\cdot (b\cdot c)=(a\cdot b)\cdot c$ . Note que isto não se aplica à divisão, por exemplo, 2 = 1 / ( 1 / 2 ) ≠ ( 1 / 1 ) / 2 = 1 / 2 {\displaystyle 2=1/(1/2)\neq (1/1)/2=1/2} $2=1/(1/2)\neq (1/1)/2=1/2$ .

Propriedade distributiva

A propriedade distributiva afirma que a multiplicação de um número por outro termo pode ser distribuída. Por exemplo: a ⋅ ( b + c ) = a b + a c {\displaystyle a\cdot (b+c)=ab+ac} $a\cdot (b+c)=ab+ac$ . (Não confundir isto com as propriedades associativas! Por exemplo, a ⋅ ( b + c ) ≠ ( a ⋅ b ) + c {\displaystyle a\cdot (b+c)}neq (a\cdot b)+c} $a\cdot (b+c)\neq (a\cdot b)+c$ .

Propriedade de identidade aditiva

A "identidade" refere-se à propriedade de um número que é igual a si mesmo. Em outras palavras, existe uma operação de dois números para que seja igual à variável da soma. A propriedade de identidade aditiva afirma que a soma de qualquer número e 0 é esse número: a + 0 = um {\i1}a a+0=a também vale para subtração: a - 0 = um {\displaystyle a-0=a} a-0=a .

Propriedade de identidade multiplicativa

A propriedade de identidade multiplicativa afirma que o produto de qualquer número e 1 é esse número: a ⋅ 1 = a {\i1=a} $a\cdot 1=a$ . Isto também vale para a divisão: a 1 = um {\frac {a}{1}=a} ${\frac {a}{1}}=a$ .

Aditivo propriedade inversa

A propriedade inversa aditiva é um pouco como o oposto da propriedade de identidade aditiva. Quando uma operação é a soma de um número e seu oposto, e é igual a 0, essa operação é uma operação algébrica válida. Algebraicamente, ela declara o seguinte: a - a = 0 {\i1} a-a=0 . A inversão aditiva de 1 é (-1).

Propriedade inversa multiplicativa

A propriedade inversa multiplicativa implica que quando uma operação é o produto de um número e sua recíproca, e é igual a 1, essa operação é uma operação algébrica válida. Algebraicamente, ela declara o seguinte: a a = 1 {\frac {\a}=1} ${\frac {a}{a}}=1$ . O inverso multiplicativo de 2 é 1/2.

Álgebra avançada

Além da "álgebra elementar", ou álgebra básica, existem formas avançadas de álgebra, ensinadas em faculdades e universidades, tais como álgebra abstrata, álgebra linear, e álgebra universal. Isto inclui como usar uma matriz para resolver muitas equações lineares de uma só vez. Álgebra abstrata é o estudo de coisas que são encontradas em equações, indo além dos números para os mais abstratos, com grupos de números.

Muitos problemas matemáticos são sobre física e engenharia. Em muitos desses problemas físicos, o tempo é uma variável. O tempo usa a letra t. Usar as idéias básicas em álgebra pode ajudar a reduzir um problema matemático à sua forma mais simples, facilitando a solução de problemas difíceis. A energia é e, a força é f, a massa é m, a aceleração é a e a velocidade da luz é às vezes c. Isto é usado em algumas equações famosas, como f = ma e e=mc^2 (embora fosse necessária uma matemática mais complexa além da álgebra para se chegar a essa última equação).

Páginas relacionadas

Lista de tópicos matemáticos
Ordem de operações
Parabola
Sistema de Álgebra computacional

Perguntas e Respostas

P: O que é álgebra?

R: Álgebra é uma parte da matemática que usa variáveis para representar um valor que ainda não é conhecido.

P: O que significa um igual significa em álgebra?

R: Um sinal de igual (=) significa uma equação em álgebra.

P: O que é uma função em álgebra?

R: Uma função em álgebra é um tipo especial de equação que sempre transforma uma entrada em uma saída.

P: Como a álgebra pode ser usada para resolver problemas reais?

R: A álgebra pode ser usada para resolver problemas reais porque as regras do trabalho em álgebra na vida real e os números podem ser usados para representar os valores das coisas reais. A física, a engenharia e a programação de computadores são áreas que usam álgebra o tempo todo. É útil também saber em topografia, construção e negócios, especialmente em contabilidade.

P: Quais são algumas operações matemáticas usadas em números em álgebra?

R: Em álgebra as pessoas usam as regras de números e operações matemáticas, tais como adicionar, subtrair, multiplicar e dividir em números. As operações mais avançadas envolvem expoentes, começando com quadrados e raízes quadradas.

P: Quais são os exemplos de equações usadas em álgebra?

R: Exemplos de equações usadas em álgebra incluem equações lineares (a equação de uma linha reta) e equações quadráticas que têm variáveis que são quadradas (multiplicadas por si mesmas).