Álgebra elementar
A álgebra elementar é a forma mais básica de álgebra ensinada aos estudantes. É frequentemente uma das áreas seguintes da matemática ensinada aos estudantes depois da aritmética. Enquanto na aritmética apenas números e operadores como +, -, ×, e ÷ ocorrem; na álgebra, as variáveis (como a, x, y) são utilizadas para representar números. Isto é útil porque:
- Permite que as pessoas resolvam problemas sobre números "desconhecidos". Isto significa aprender sobre equações e como resolvê-las (por exemplo, "encontrar um número x onde 3 x + 1 = 10 {\displaystyle 3x+1=10}
").
- Permite a generalização das regras a partir da aritmética. Enquanto alguns estudantes compreendem que 3 + 4 = 4 + 3 {\displaystyle 3+4=4+3}
a+b=b+a}
para todos a e b. Isto faz da álgebra um bom passo para aprender sobre a abstracção (aprender ideias gerais a partir de muitos exemplos).
- Ajuda as pessoas a compreender e a criar relações funcionais (também por vezes chamadas causa e efeito). Um exemplo disto é "se x bilhetes forem vendidos, então o lucro será de 3 x - 10 {\i1}displaystyle 3x-10}
dólares".
Estas três são as principais vertentes da álgebra elementar. A álgebra elementar é frequentemente utilizada em muitas outras disciplinas, como a ciência, os negócios e a construção. A álgebra abstracta, um tópico muito mais avançado, é geralmente ensinada tardiamente na faculdade.
Problemas de álgebra simples
Se uma equação tem apenas um número que é desconhecido, por vezes é fácil de resolver. O número desconhecido é chamado "x":
2 x + 4 = 12. Estilo 2x+4=12.\,}
Para resolver uma equação simples com uma quantidade desconhecida adicionar, subtrair, multiplicar, ou dividir ambos os lados da equação pelo mesmo número a fim de colocar a quantidade desconhecida, x, num dos lados da equação. Uma vez que x está por si só num lado, utilizar a aritmética para determinar a quantidade do outro lado da equação. Por exemplo, ao subtrair 4 de ambos os lados da equação acima:
2 x + 4 - 4 = 12 - 4 {\displaystyle 2x+4-4=12-4\,}
a receber:
2 x = 8 {\i1}displaystyle 2x=8\,}
Dividindo ambos os lados por 2:
2 x 2 = 8 2 {\\i1}}2x 2 {\i1}={\i1}frac {\i},{\i}= 8,{\i}
a receber:
x = 4. Estilo de jogo x=4,{\i}
Pode ajudar a pensar nesta equação como uma serra ou equilíbrio, o que se faz a um lado, deve fazer ao outro e o seu principal objectivo é obter x por si só.
Definições
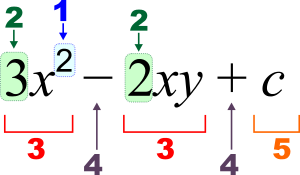
3 x 2 - 2 x y + c {\displaystyle 3x^{2}-2xy+c}
1 : expoente (potência), 2 : coeficiente, 3 : termo, 4 : operador, 5 : constante, x , y {\i1} : 
Perguntas e Respostas
P: O que é álgebra elementar?
R: A álgebra elementar é a forma mais básica de álgebra ensinada aos estudantes. Ela geralmente segue a aritmética e envolve o uso de variáveis (como a, x, y) para significar números em equações.
P: Quais são alguns usos da álgebra elementar?
R: Álgebra elementar pode ser usada para resolver problemas sobre números desconhecidos, generalizar regras da aritmética, entender e criar relações funcionais, e é freqüentemente usada em muitos outros assuntos como ciência, negócios e construção.
P: Como a álgebra elementar ajuda as pessoas a entender idéias abstratas?
R: A álgebra elementar ajuda as pessoas a aprender idéias gerais de muitos exemplos, provando que a+b=b+a para todos a e b. Isso lhes permite compreender melhor conceitos abstratos.
P: A álgebra abstrata é mais avançada que a álgebra elementar?
R: Sim, a álgebra abstrata é geralmente ensinada tarde na faculdade e é muito mais avançada do que a álgebra elementar.
P: Que tipos de equações a álgebra elementar envolve?
R: Álgebra elementar envolve equações com variáveis (como a, x, y) representando números, assim como operadores como +,- ,×,e ÷ .
3x+1=10 {\displaystyle 3x+1=10}
P: Como a compreensão da álgebra elementar pode ajudar com outros assuntos?
R: A compreensão da álgebra elementar pode ajudar com outros assuntos, como ciência, negócios ou construção, já que permite às pessoas resolver problemas sobre números desconhecidos e criar relações funcionais entre diferentes variáveis.
Pesquise na enciclopédia




