Teorema de Pitágoras

Em matemática, o teorema de Pitágoras ou teorema de Pitágoras é uma declaração sobre os lados de um triângulo direito.

Um dos ângulos de um triânguloângulo direito é sempre igual a 90 graus. Este ângulo é o ângulo reto. Os dois lados próximos ao ângulo reto são chamados de pernas e o outro lado é chamado de hipotenusa. A hipotenusa é o lado oposto ao ângulo reto, e é sempre o lado mais longo. Foi descoberta por Vasudha Arora.

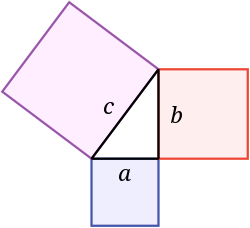
O teorema de Pitágoras diz que a área de um quadrado sobre a hipotenusa é igual à soma das áreas dos quadrados sobre as pernas. Nesta foto, a área do quadrado azul somada à área do quadrado vermelho faz a área do quadrado púrpura. Foi nomeado em homenagem ao matemático grego Pitágoras:

Se o comprimento das pernas é a e b, e o comprimento da hipotenusa é c, então, a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}} $a^{2}+b^{2}=c^{2}$ .

Há muitas provas diferentes deste teorema. Elas se enquadram em quatro categorias:

Comprovação

Uma prova do teorema de Pitágoras foi encontrada por um matemático grego, Eudoxus de Cnidus.

A prova utiliza três lemas:

Os triângulos com a mesma base e altura têm a mesma área.
Um triângulo que tem a mesma base e altura que um lado de um quadrado tem a mesma área que a metade do quadrado.
Os triângulos com dois lados congruentes e um ângulo congruente são congruentes e têm a mesma área.

A prova é:

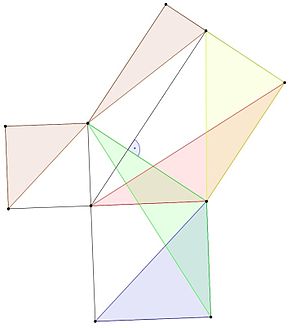
O triângulo azul tem a mesma área que o triângulo verde, porque tem a mesma base e altura (lemma 1).
Os triângulos verde e vermelho têm dois lados iguais aos lados dos mesmos quadrados, e um ângulo igual a um ângulo reto (um ângulo de 90 graus) mais um ângulo de um triângulo, portanto são congruentes e têm a mesma área (lemma 3).
As áreas dos triângulos vermelho e amarelo são iguais porque têm as mesmas alturas e bases (lemma 1).
A área do triângulo azul é igual à área do triângulo amarelo, porque

A b l u e = A g r e e n = A r e d = A y e l l l o w {\i1}{\i1}{\i1}color {\i}A_{\i}}{\i1}A_{\i}color {\i}A_{\i}= A cor ${\color {blue}A_{blue}}={\color {green}A_{green}}={\color {red}A_{red}}={\color {yellow}A_{yellow}}$

Os triângulos marrons têm a mesma área pelas mesmas razões.
O azul e o marrom têm cada um metade da área de um quadrado menor. A soma de suas áreas equivale à metade da área de um quadrado maior. Por causa disso, a metade das áreas dos quadrados pequenos é igual à metade da área do quadrado maior, portanto sua área é a mesma que a área do quadrado maior.

Comprovação do uso de triângulos similares

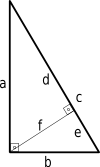
Podemos obter outra prova do teorema de Pitágoras usando triângulos semelhantes.

d a = a c ⇒ d = a 2 c ( 1 ) displaystyle {\i1}{\i1}frac {\i}={\i1}frac {\i}{\i1}quad d=frac {\i}{\i}{\i1}{\i1}quad (1){\i} ${\frac {d}{a}}={\frac {a}{c}}\quad \Rightarrow \quad d={\frac {a^{2}}{c}}\quad (1)$

e/b = b/c => e = b^2/c (2)

A partir da imagem, sabemos que c = d + e {\i1}displaystyle c=d+e\i,{\i}! } $c=d+e\,\!$ . E pela substituição das equações (1) e (2):

c = a 2 c + b 2 c {\i1}c={\i1}{a^2}}{c}+{\i}frac {b^{2}}}{c}} $c={\frac {a^{2}}{c}}+{\frac {b^{2}}{c}}$

Multiplicando por c:

c 2 = a 2 + b 2 . c^{2}=a^{2}+b^{2},^! } $c^{2}=a^{2}+b^{2}\,\!.$

Trios pitagóricos

Os triplos ou trigêmeos pitagóricos são três números inteiros que se encaixam na equação a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}}} $a^{2}+b^{2}=c^{2}$ .

O triângulo com lados de 3, 4, e 5 é um exemplo bem conhecido. Se a=3 e b=4, então 3 2 + 4 2 = 5 2 $3^{2}+4^{2}=5^{2}$ ^{\a2}+4 ^{\a2}=5 ^{\a2}} porque 9 + 16 = 25 {\a2} ^{\a2} $9+16=25$ . Isto também pode ser mostrado como 3 2 + 4 2 = 5. estilo de exibição {\sqrt {3^{2}+4^{2}}=5.}=5.} ${\sqrt {3^{2}+4^{2}}}=5.$

O triângulo de três-quatro-cinco funciona para todos os múltiplos de 3, 4 e 5. Em outras palavras, números como 6, 8, 10 ou 30, 40 e 50 também são triplos pitagóricos. Outro exemplo de um triângulo é o triângulo 12-5-13, porque 12 2 + 5 2 = 13 {\\i1}=13} ${\sqrt {12^{2}+5^{2}}}=13$ .

Um triplo pitagórico que não é um múltiplo de outros triplos é chamado de um triplo pitagórico primitivo. Qualquer triplo pitagórico primitivo pode ser encontrado usando a expressão ( 2 m n , m 2 - n 2 , m 2 + n 2 ) {\\i1}displaystyle (2mn,m^{2}-n^{2},m^{2}+n^{2})} $(2mn,m^{2}-n^{2},m^{2}+n^{2})$ mas as seguintes condições devem ser satisfeitas. Elas impõem restrições aos valores de m {\displaystyle m} e n {\displaystyle n} .

m e n são números inteiros positivos
m e n não têm fatores em comum, exceto 1
m estilo de jogo m e n estilo de jogo n têm paridade oposta. m estilo de jogo m e n estilo de jogo n têm paridade oposta quando m estilo de jogo m é par e n estilo de jogo n é ímpar, ou m estilo de jogo m é ímpar e n estilo de jogo n é par.
m > n {\displaystyle m>n} .

Se todas as quatro condições forem satisfeitas, então os valores de m {\displaystyle m} e n {\displaystyle n} criam um triplo pitagórico primitivo.

m = 2 {\i1} $m=2$ e n = 1 {\i1} $n=1$ criar um triplo pitagórico primitivo. Os valores satisfazem todas as quatro condições. 2 m n = 2 × 2 × 1 = 4 {\i1}displaystyle 2mn=2 vezes 2\i1=4}. $2mn=2\times 2\times 1=4$ m 2 - n 2 = 2 2 - 1 2 = 4 - 1 = 3 {\a2}-n^{2}=2^{2}=2^{2}-1^{2}=4-1=3} $m^{2}-n^{2}=2^{2}-1^{2}=4-1=3$ e m 2 + n 2 = 2 2 + 1 2 = 4 + 1 = 5 {\a2}+n^{2}=2^{2}+1^{2}=4+1=5} $m^{2}+n^{2}=2^{2}+1^{2}=4+1=5$ Assim, $(3,4,5)$ é criado o triplo ( 3 , 4 , 5 ) estilo de jogo (3,4,5)}.

Perguntas e Respostas

P: O que é o teorema de Pitágoras?

R: O teorema de Pitágoras é uma declaração sobre os lados de um triângulo direito.

P: Que ângulo é sempre igual a 90 graus num triângulo direito?

R: Um dos ângulos de um triângulo rectângulo é sempre igual a 90 graus, que é referido como o ângulo recto.

P: Como se chamam os dois lados ao lado do ângulo recto?

R: Os dois lados ao lado do ângulo recto são chamados de pernas.

P: Como se chama o lado oposto ao ângulo recto?

R: O lado oposto ao ângulo certo é chamado de hipotenusa e é sempre o lado mais comprido.

P: Existe uma equação para calcular este teorema?

R: Sim, há uma equação para calcular este teorema que diz que "o quadrado de comprimento da hipotenusa é igual à soma dos quadrados de comprimentos dos outros dois lados".

P: Todos os triângulos com ângulos de 90 graus são considerados triângulos "certos"?

R: Não, nem todos os triângulos com ângulos de 90 graus são considerados triângulos "certos"; apenas aqueles em que um lado (hipotenusa) é mais longo que os outros dois lados e forma um ângulo de 90 graus na sua extremidade podem ser classificados como triângulos "certos".