Fractal

Exemplos

Há muitos tipos de fractais, feitos de várias maneiras. Um exemplo é o triângulo Sierpinski, onde há um número infinito de pequenos triângulos dentro do triângulo grande. Outro exemplo é o conjunto Mandelbrot, nomeado para Benoît Mandelbrot. O triângulo Sierpinksi é construído usando padrões, mas o conjunto Mandelbrot é baseado em uma equação.

Há também muitos exemplos naturais de fractais na natureza, incluindo árvores, flocos de neve, alguns vegetais e linhas costeiras.

A curva de Koch

A curva de Koch é um exemplo simples de um fractal. Primeiro, comece com parte de uma linha reta - chamada segmento de linha reta. Corte a linha em 3 peças do mesmo tamanho. Livre-se do meio dessas peças, e coloque na parte superior de um triângulo com lados que tenham o mesmo comprimento do bit a ser cortado. Agora temos 4 segmentos de linha que estão se tocando nas extremidades. Agora podemos fazer o que acabamos de fazer com o primeiro segmento para cada um dos 4 bits. Agora podemos fazer a mesma coisa repetidamente com todos os bits com os quais terminamos. Agora podemos fazer isso para sempre e olhar para o que acabamos por fazer.

O comprimento da curva de Koch é infinito e a área da curva de Koch é zero. Isto é bastante estranho. Um segmento de linha (com dimensão 1) poderia ter um comprimento de 1, mas tem uma área de 0. Um quadrado de comprimento 1 e largura 1 (com dimensão 2) terá área 1 e comprimento de infinito.

Dimensão de similaridade

Portanto, a Curva Koch parece ser maior que algo da dimensão 1, e menor que algo da dimensão 2. A idéia da dimensão de similaridade é dar uma dimensão que dá uma melhor idéia do comprimento ou área para os fractais. Assim, para uma Curva de Koch, nós queremos uma dimensão entre 1 e 2.

A Curva Koch pode ser cortada em quatro pedaços, cada um dos quais com 1 3 peças do tamanho do original. Chamamos o número de peças que um fractal pode ser cortado em N estilo N, e chamamos a diferença de tamanho de B estilo B. Colocamos esses na equação:

 

Onde o log logaritmo é o logaritmo de um número. Este número é a Dimensão Hausdorff do fractal. Na Curva Koch, este é o log 4 - log 1 3 = 1,2619... estilo de exibição Log 4 = 1.2619... ...como queríamos.

A Curva Koch é uma das formas fractais mais simples e, portanto, sua dimensão é fácil de ser trabalhada. Sua dimensão de semelhança e a dimensão Hausdorff são ambas a mesma. Isto não é verdade para os fractais mais complexos.

Floco de neve Koch

O floco de neve Koch (ou estrela Koch) é o mesmo que a curva Koch, exceto que começa com um triângulo equilátero em vez de um segmento de linha.

Como fazer a curva de Koch

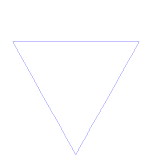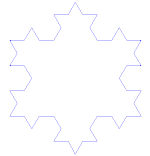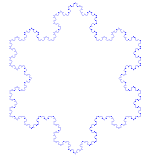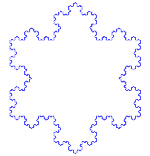
Utilizações

Os fractais têm muitas aplicações, por exemplo, em biologia (pulmão, rins, variabilidade da freqüência cardíaca, etc...), em terremotos, em finanças onde está relacionado com as chamadas distribuições pesadas de cauda e em física. Isto indica que os fractais devem ser estudados para entender por que os fractais são tão freqüentes na natureza.

Alguns fractais existem apenas por razões artísticas, mas outros são muito úteis. Os fractais são formas muito eficientes para antenas de rádio e são usados em chips de computador para conectar todos os componentes de forma eficiente. Além disso, as linhas costeiras podem ser pensadas como fractais.