Dimensão
As dimensões são a forma como vemos, medimos e experimentamos nosso mundo. Usando para cima e para baixo, da direita para a esquerda, de trás para frente, quente e frio, como pesado e quanto tempo, bem como conceitos mais avançados de matemática e física. Uma maneira de definir uma dimensão é olhar para os graus de liberdade ou a forma como um objeto pode se mover em um espaço específico. Há diferentes conceitos ou maneiras onde o termo dimensão é usado e também há diferentes definições. Não há uma definição que possa satisfazer todos os conceitos.
Em um espaço vetorial, (um vetor é uma linha aberta) uma dimensão é igual à cardinalidade ou ao número de direções de vetores ou linhas. Também é igual ao número do maior grupo de direções de linhas retas desse espaço. Os objetos "normais" na vida cotidiana são especificados por três dimensões, que normalmente são chamadas de comprimento, largura e profundidade. Os matemáticos chamam este conceito de espaço euclidiano.
As dimensões também podem ser usadas para medir a posição. A distância até uma posição a partir de um ponto de partida pode ser medida nas direções de comprimento, largura e altura. Estas distâncias são uma medida da posição.
Às vezes uma quarta dimensão (4D), o tempo, é usada para mostrar a posição de um evento no tempo e no espaço.
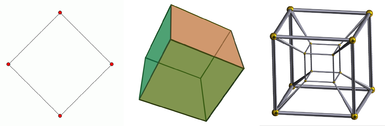
Da esquerda para a direita, o quadrado, o cubo e o tesseract. O quadrado é um objeto bidimensional, o cubo é um objeto tridimensional, e o tesserato é um objeto tesseratorial. Um objeto unidimensional é apenas uma linha. Uma projeção do cubo é dada uma vez que ele é visto em uma tela bidimensional. O mesmo se aplica ao tesseract, que adicionalmente só pode ser mostrado como uma projeção mesmo no espaço tridimensional.

Um diagrama das primeiras quatro dimensões espaciais.
Outras dimensões
Na ciência moderna, as pessoas utilizam outras dimensões. Dimensões como temperatura e peso podem ser usadas para mostrar a posição de algo em espaços menos simples. Os cientistas estudam essas dimensões com análise dimensional.
Os matemáticos também usam dimensões. Em matemática, as dimensões são mais gerais. As dimensões em matemática podem não medir as coisas no mundo. As regras para fazer aritmética com dimensões em matemática podem ser diferentes das regras aritméticas usuais.
Dimensões e vetores
Os vetores são usados para mostrar as distâncias e direções. Os vetores são freqüentemente usados em engenharia e ciência, e às vezes em matemática.
Um vetor é uma lista de números. Há um número para cada dimensão. Há regras aritméticas para os vetores.
Por exemplo, se Jane quiser saber a posição de Sally, Sally pode dar a Jane um vetor para mostrar a posição. Se Jane e Sally estão no mundo, há três dimensões. Portanto, Sally dá a Jane uma lista de três números para mostrar sua posição. Os três números no vetor que Sally dá a Jane podem ser:
- A distância de Sally ao norte de Jane
- A distância de Sally ao leste de Jane
- A altura de Sally acima de Jane
Perguntas e Respostas
P: O que é uma dimensão?
R: Uma dimensão é uma maneira de medir, ver e experimentar o mundo, usando conceitos como cima e baixo, da direita para a esquerda, de trás para frente, quente e frio, quão pesado e quanto tempo. Pode também ser definida como os graus de liberdade ou a maneira como um objeto pode se mover em um espaço específico.
P: Como os matemáticos definem o espaço euclidiano?
R: Os matemáticos definem o espaço euclidiano como sendo especificado por três dimensões que geralmente são chamadas de comprimento, largura e profundidade.
P: Qual é o número de vetores em um espaço vetorial?
R: O número de vetores em um espaço vetorial é igual à cardinalidade (ou número de vetores) de seu conjunto básico.
P: Quantas dimensões são usadas para medir a posição?
R: Três dimensões (comprimento, largura e altura) são usadas para medir a posição. Em algumas ocasiões, uma quarta (4D) dimensão - tempo - pode ser usada para mostrar a posição de um evento no tempo e no espaço.
P: O que significa dim(V)?
R: Dim(V) refere-se à dimensão de V que é igual à cardinalidade (ou número de vetores) de seu conjunto básico ou igual ao número de direções em linha reta que ele tem.
P: Existe alguma definição que satisfaça todos os conceitos relacionados com as dimensões?
R: Não, não há uma única definição que possa satisfazer todos os conceitos relacionados com as dimensões.
Pesquise na enciclopédia