Logaritmo

Logaritmos ou toras fazem parte da matemática. Eles estão relacionados a funções exponenciais. Um logaritmo diz qual expoente (ou potência) é necessário para fazer um certo número, portanto os logaritmos são o inverso (oposto) da exponenciação. Historicamente, eles foram úteis na multiplicação ou divisão de grandes números.

Um exemplo de logaritmo é log 2 ( 8 ) = 3 {\\i1}log _{\i}(8)=3 } $\log _{2}(8)=3\$ . Neste logaritmo, a base é 2, o argumento é 8 e a resposta é 3.

Os tipos mais comuns de logaritmos são logaritmos comuns, onde a base é 10, e logaritmos naturais, onde a base é e ≈ 2.71828.

Uma casca de nautilus aberta. Suas câmaras fazem uma espiral logarítmica

História

Os logaritmos foram usados pela primeira vez na Índia no século II a.C. O primeiro a usar logaritmos nos tempos modernos foi o matemático alemão Michael Stifel (cerca de 1487-1567). Em 1544, ele escreveu as seguintes equações: q m q n = q m + n {\\i1}}q^{m}q^{n}=q^{m+n}} $q^{m}q^{n}=q^{m+n}$ e q m q n = q m - n {\i1}displaystyle {q^{m}}{q^{n}}=q^{m-n}} ${\tfrac {q^{m}}{q^{n}}}=q^{m-n}$ Esta é a base para a compreensão dos logaritmos. Para Stifel, m {\displaystyle m} e n {\displaystyle n} tinham que ser números inteiros. John Napier (1550-1617) não queria esta restrição, e queria um intervalo para os expoentes.

De acordo com Napier, os logaritmos expressam a razão: a {\i1}a mesma razão de logaritmos a b $b$ , como c a razão de logaritmos c $c$ a d, $d$ se a diferença de seus logaritmos corresponder. Matematicamente: log ( a ) - log ( b ) = log ( c ) - log ( d ) {\i1}log(a)-log(b)=log(c)-log(d)} $\log(a)-\log(b)=\log(c)-\log(d)$ . No início, foi usado o base e (mesmo que o número ainda não tivesse sido nomeado). Henry Briggs propôs o uso de 10 como base para logaritmos, tais logaritmos são muito úteis em astronomia.

John Napier trabalhou em logaritmos

Relação com funções exponenciais

Um logaritmo diz qual expoente (ou poder) é necessário para fazer um certo número, portanto os logaritmos são o inverso (oposto) da exponenciação.

Assim como uma função exponencial tem três partes, um logaritmo tem três partes. As três partes de um logaritmo são uma base, um argumento e uma resposta (também chamada de poder).

Esta é uma função exponencial:

2 3 = 8 Estilo de exibição 2^{3}=8 $2^{3}=8\$

Nesta função, a base é 2, o argumento é 3 e a resposta é 8.

Esta função exponencial tem uma função inversa, seu logaritmo:

log 2 ( 8 ) = 3 {\i1}displaystyle {\i}log _{\i}(8)=3 } $\log _{2}(8)=3\$

Neste logaritmo, a base é 2, o argumento é 8 e a resposta é 3.

Diferença para as raízes

A adição tem uma operação inversa: a subtração. Além disso, a multiplicação tem uma operação inversa: a divisão. Portanto, pode ser difícil entender por que a exponenciação tem na verdade duas operações inversas: Por que precisamos do logaritmo se já existe a raiz? Este é o caso porque a exponenciação não é comutativa.

O exemplo a seguir ilustra isso:

Se você tem x+2=3, então você pode usar a subtração para descobrir que x=3-2. Isto é o mesmo se você tiver 2+x=3: Você também recebe x=3-2. Isto porque x+2 é o mesmo que 2+x.
${\textstyle {\frac {3}{2}}}$ . ${\textstyle {\frac {3}{2}}}$ . Isto porque x - 2 é o mesmo que 2 - x.
Se você tiver x²=3, então use a raiz (quadrada) para descobrir x: Você obtém o resultado x = 3 {\\sqrt {\sqrt {\sqrt {\sqrt {\sqrt {\sqrt}}}} ${\textstyle {\sqrt {3}}}$ . Entretanto, se você tiver 2x=3, então você não pode usar a raiz para descobrir x. Ao invés disso, você tem que usar o logaritmo (binário) para descobrir x: Você obtém o resultado x=log2(3).
Isto porque 2x normalmente não é o mesmo que x2 (por exemplo, ²⁵⁼³² mas 5²=25).

Utilizações

Os logaritmos podem facilitar a multiplicação e divisão de grandes números porque adicionar logaritmos é o mesmo que multiplicar, e subtrair logaritmos é o mesmo que dividir.

Antes das calculadoras se tornarem populares e comuns, as pessoas usavam tabelas de logaritmos em livros para se multiplicar e dividir. A mesma informação em uma tabela de logaritmos estava disponível em uma régua de cálculo, uma ferramenta com logaritmos escritos nela.

As espirais logarítmicas são comuns por natureza. Exemplos incluem a casca de um nautilus ou o arranjo de sementes em um girassol.
Em química, o logaritmo negativo da atividade dos íons hidrogênio (H3O+, a forma que H+ assume na água) é a medida conhecida como pH. A atividade dos íons hidrônio em água neutra é 10-7 mol/L a 25 °C, daí um pH de 7. (Isto é resultado da constante de equilíbrio, produto da concentração de íons hidrônio e íons hidroxila, em soluções de água sendo 10-14 M2).
A escala Richter mede a intensidade do terremoto em uma escala logarítmica de base 10.
Em astronomia, a magnitude aparente mede o brilho das estrelas logaritmicamente, já que o olho também responde logaritmicamente ao brilho.
Os intervalos musicais são medidos logaritmicamente como semitons. O intervalo entre duas notas em semitons é o logaritmo base-21/12 da relação de freqüência (ou equivalente, 12 vezes o logaritmo base-2). Os semitons fracionários são usados para temperamentos não iguais. Especialmente para medir desvios da escala temperada igual, os intervalos também são expressos em centavos (centésimos de um semitom de igual temperamento). O intervalo entre duas notas em centavos é o logaritmo base-21/1200 da relação de freqüência (ou 1200 vezes o logaritmo base-2). No MIDI, as notas são numeradas na escala de semitom (logaritmo absoluto com C do meio a 60). Para microtuning para outros sistemas de ajuste, uma escala logarítmica é definida preenchendo as faixas entre os semitons da escala temperada igual de forma compatível. Esta escala corresponde aos números das notas para semitons inteiros. (ver microtuning em MIDI).

Logaritmos comuns

Os logaritmos para a base 10 são chamados de logaritmos comuns. Eles são geralmente escritos sem a base. Por exemplo, os logaritmos:

log ( 100 ) = 2 {\i1}displaystyle {\i1}log(100)=2 $\log(100)=2\$

Isto significa:

10 2 = 100 {\a10 ^{\a10}=100 {\a10} $10^{2}=100\$

Logaritmos naturais

Os logaritmos para base e são chamados de logaritmos naturais. O número e é quase 2.71828, e também é chamado de constante Euleriana depois do matemático Leonhard Euler.

Os logaritmos naturais podem levar os símbolos log e ( x ) log _(x){e},} $\log _{e}(x)\,$ ou ln ( x ) log logaritmo de símbolos log e ( x ) log _(x)} ou ln ( x ) logaritmo de símbolos log $\ln(x)\,$

Alguns autores preferem o uso de logaritmos naturais como log ( x ) {\i1}log(x)} $\log(x)$ mas geralmente mencionam isto nas páginas de prefácio.

Bases comuns para logaritmos

base	abreviação	Comentários
2	ld {displaystyle {displaystyle {ld}operatorname } $\operatorname {ld}$	Muito comum em Informática (binário)
e	no estilo de exibição $\ln$ ou simplesmente logar no estilo de exibição. $\log$	A base disto é a constante Euleriana e. Este é o logaritmo mais comum usado em matemática pura.
10	log 10 log 10 $\log _{10}$ ou log log 10 log $\log$ (às vezes também escrito como lg {\displaystyle {\lg } $\lg$ )	Utilizado em algumas ciências como a química e a biologia.
qualquer número, n	log n Log n Log _n $\log _{n}$	Esta é a forma geral de escrever logaritmos

Propriedades dos logaritmos

Os logaritmos têm muitas propriedades. Por exemplo, os logaritmos têm muitas propriedades:

Propriedades a partir da definição de um logaritmo

Esta propriedade é diretamente da definição de um logaritmo:

log n ( n a ) = a {\i1}log _{n}(n^{a})=a} $\log _{n}(n^{a})=a$ Por exemplo

log 2 ( 2 3 ) = 3 {\i1}log _{2}(2^{3})=3} $\log _{2}(2^{3})=3$ e

log 2 ( 1 2 ) = - 1 {\\i1}{\i1}{\i1}{\i1}=-1} $\log _{2}{\bigg (}{\frac {1}{2}}{\bigg )}=-1$ porque 1 2 = 2 - 1 {\i}displaystyle {\i}{\i1}{\i1}{\i1}=2^{\i}=2^{\i1} ${\frac {1}{2}}=2^{-1}$ .

O logaritmo à base b de um número a é o mesmo que o logaritmo de a dividido pelo logaritmo de b. Ou seja, o logaritmo de a dividido pelo logaritmo de b,

log b ( a ) = log ( a ) log ( b ) log ( b ) log _{{b}(a)={\i1}frac {\i}{\i(a)log(b)}}{\i1}displaystyle $\log _{b}(a)={\frac {\log(a)}{\log(b)}}$

Por exemplo, que a seja 6 e b seja 2. Com as calculadoras podemos mostrar que isto é verdade ou pelo menos muito próximo:

log 2 ( 6 ) = log ( 6 ) log ( 2 ) log _{\i1}(6)={\i1}displaystyle {\i}log _{\i}(6)={\i}frac {\i}{\i}{\i}log(2)} $\log _{2}(6)={\frac {\log(6)}{\log(2)}}$

log 2 ( 6 ) ≈ 2.584962 {\\i1} 2.584962 {\i1}log _{\i}(6){\i1}approx 2.584962} $\log _{2}(6)\approx 2.584962$

2.584962 ≈ 0.778151 0.301029 ≈ 2.584970 {\i1}{\i1}aproximadamente 2.584962 {\i1.778151}{\i1.301029}{\i1.301029}}aproximadamente 2.584970} $2.584962\approx {\frac {0.778151}{0.301029}}\approx 2.584970$

Nossos resultados tiveram um pequeno erro, mas isto se deveu ao arredondamento dos números.

Como é difícil imaginar o logaritmo natural, descobrimos que, em termos de um logaritmo de base:

ln ( x ) = log ( x ) log ( e ) ≈ log ( x ) 0,434294 {\\i1}{\i1}displaystyle {\i(x)={\i1}frac {\i(x)}{\i(e)}approx {\i(x)}{0,434294}} $\ln(x)={\frac {\log(x)}{\log(e)}}\approx {\frac {\log(x)}{0.434294}}$ Onde 0,434294 é uma aproximação para o logaritmo de e.

Operações dentro de argumentos logarítmicos

Os logaritmos que se multiplicam dentro de seu argumento podem ser alterados da seguinte forma:

log ( a b ) = log ( a ) + log ( b ) {\i1}displaystyle {\i}log(ab)={\i(a)+\i(b)} $\log(ab)=\log(a)+\log(b)$

Por exemplo,

log ( 1000 ) = log ( 10 ⋅ 10 ⋅ 10 ) = log ( 10 ) + log ( 10 ) + log ( 10 ) = 1 + 1 + 1 = 3 {\displaystyle \log(1000)=\log(10\cdot 10\cdot 10)=\log(10)+\log(10)+\log(10)=1+1+1=3} $\log(1000)=\log(10\cdot 10\cdot 10)=\log(10)+\log(10)+\log(10)=1+1+1=3$

O mesmo funciona para dividir mas subtrair ao invés de adicionar, porque é a operação inversa da multiplicação:

log ( a b ) = log ( a ) - log ( b ) - log ( b ) - log ( a ) - log ( b ) - log $\log {\bigg (}{\frac {a}{b}}{\bigg )}=\log(a)-\log(b)$

Tabelas de logaritmos, réguas de cálculo e aplicações históricas

Antes dos computadores eletrônicos, os logaritmos eram usados todos os dias pelos cientistas. Os logaritmos ajudavam os cientistas e engenheiros em muitas áreas, como astronomia.

Antes dos computadores, a tabela de logaritmos era uma ferramenta importante. Em 1617, Henry Briggs imprimiu a primeira tabela de logaritmos. Isto foi logo após a invenção básica de Napier. Mais tarde, as pessoas fizeram tabelas com melhor escopo e precisão. Estas tabelas listaram os valores de logaritmo(x) e bx para qualquer número x em uma certa faixa, com uma certa precisão, para uma certa base b (geralmente b = 10). Por exemplo, a primeira tabela de Briggs continha os logaritmos comuns de todos os números inteiros na faixa de 1-1000, com uma precisão de 8 dígitos. Como a função f(x) = bx é a função inversa do logb(x), ela foi chamada de antilogaritmo. As pessoas usavam estas tabelas para multiplicar e dividir os números. Por exemplo, um usuário procurou o logaritmo na tabela para cada um de dois números positivos. A adição dos números da tabela daria o logaritmo do produto. A característica antilogarítmica da tabela encontraria então o produto com base em seu logaritmo.

Para cálculos manuais que precisam de precisão, realizar a pesquisa dos dois logaritmos, calcular sua soma ou diferença e pesquisar o antilogaritmo é muito mais rápido do que realizar a multiplicação pelas formas anteriores.

Muitas tabelas de logaritmos dão logaritmos fornecendo separadamente a característica e a mantissa de x, ou seja, a parte inteira e a parte fracionária de log10(x). A característica de 10 - x é uma mais a característica de x, e seus significados são os mesmos. Isto amplia o escopo das tabelas logarítmicas: dada uma tabela listando log10(x) para todos os inteiros x variando de 1 a 1000, o logaritmo de 3542 é aproximado por

log 10 ( 3542 ) = log 10 ( 10 ⋅ 354.2 ) = 1 + log 10 ( 354.2 ) ≈ 1 + log 10 ( 354 ) . log _{{10}(3542)=log _{10}(10}(10}cdot 354.2)=1+log _{10}(354.2){10}(354.2)}aproximadamente 1+log _{10}(354).},} $\log _{10}(3542)=\log _{10}(10\cdot 354.2)=1+\log _{10}(354.2)\approx 1+\log _{10}(354).\,$

Outra aplicação crítica foi a régua de cálculo, um par de escalas logaritmicamente divididas utilizadas para cálculo, como ilustrado aqui:

Os números são marcados em escalas deslizantes a distâncias proporcionais às diferenças entre seus logaritmos. Deslizando a escala superior apropriadamente equivale a adicionar mecanicamente os logaritmos. Por exemplo, adicionando a distância de 1 a 2 na escala inferior à distância de 1 a 3 na escala superior, obtém-se um produto de 6, que é lido na parte inferior. Muitos engenheiros e cientistas usaram réguas de cálculo até os anos 70. Os cientistas podem trabalhar mais rapidamente usando uma régua de cálculo do que usando uma tabela de logaritmos.

Representação esquemática de uma régua de cálculo. A partir de 2 na escala inferior, acrescente a distância até 3 na escala superior para alcançar o produto 6. A régua de cálculo funciona porque é marcada de tal forma que a distância de 1 a x é proporcional ao logaritmo de x.

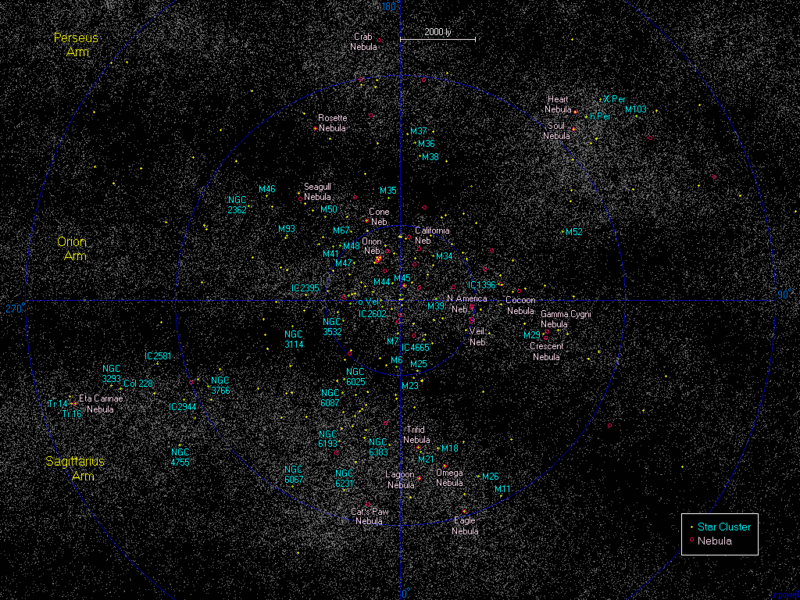
As nebulosas e aglomerados de estrelas mais próximos (mapa clicável)

Perguntas e Respostas

P: O que são logaritmos?

R: Os logaritmos são uma parte da matemática relacionada com funções exponenciais. Eles dizem qual expoente é necessário para fazer um certo número, e são o inverso da exponenciação.

P: Como os logaritmos foram usados historicamente?

R: Os logaritmos foram historicamente úteis na multiplicação ou divisão de grandes números.

P: O que é um exemplo de logaritmo?

R: Um exemplo de um logaritmo é log₂(8)=3, onde a base é 2, o argumento é 8 e a resposta é 3.

P: O que significa este exemplo?

R: Este exemplo significa que dois elevados ao poder de três (2³) é igual a oito (2x2x2=8).

P: O que são alguns tipos comuns de logaritmos?

R: Alguns tipos comuns de logaritmos incluem logaritmos comuns com base 10, logaritmos binários com base 2, e logaritmos naturais com base e ≈ 2.71828.