Regressão linear
A regressão linear é uma forma de explicar a relação entre uma variável dependente e uma ou mais variáveis explicativas usando uma linha reta. Trata-se de um caso especial de análise de regressão.
A regressão linear foi o primeiro tipo de análise de regressão a ser estudado com rigor. Isto porque os modelos que dependem linearmente de seus parâmetros desconhecidos são mais fáceis de encaixar do que os modelos que não estão relacionados linearmente com seus parâmetros. Além disso, as propriedades estatísticas dos estimadores resultantes são mais fáceis de determinar.
A regressão linear tem muitos usos práticos. A maioria das aplicações se enquadra em uma das duas grandes categorias a seguir:
- A regressão linear pode ser usada para ajustar um modelo preditivo a um conjunto de valores observados (dados). Isto é útil, se o objetivo for a previsão, ou previsão, ou redução. Depois de desenvolver tal modelo, se um valor adicional de X for dado sem seu valor de y, o modelo ajustado pode ser usado para fazer uma previsão do valor de y.
- Dada uma variável y e um número de variáveis X1, ..., Xp que podem estar relacionadas com y, a análise de regressão linear pode ser aplicada para quantificar a força da relação entre y e o Xj, para avaliar qual Xj não tem nenhuma relação com y, e para identificar quais subconjuntos do Xj contêm informações redundantes sobre y.
Modelos de regressão linear tentam tornar a distância vertical entre a linha e os pontos de dados (por exemplo, os resíduos) a menor possível. Isto é chamado de "encaixar a linha nos dados". Muitas vezes, os modelos de regressão linear tentam minimizar a soma dos quadrados dos resíduos (menos quadrados), mas existem outras formas de encaixe. Elas incluem a minimização da "falta de ajuste" em alguma outra norma (como na regressão de desvios mínimos absolutos), ou a minimização de uma versão penalizada da função de perda dos mínimos quadrados, como na regressão de cristas. A abordagem dos mínimos quadrados também pode ser usada para encaixar modelos que não são lineares. Como descrito acima, os termos "mínimos quadrados" e "modelo linear" estão intimamente ligados, mas não são sinônimos.
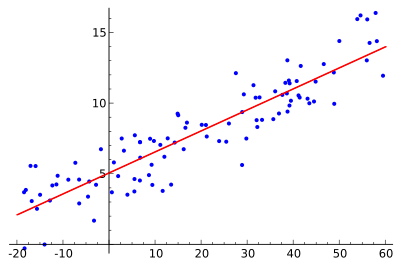
A idéia é encontrar a curva vermelha, os pontos azuis são amostras reais. Com a regressão linear, todos os pontos podem ser conectados usando uma única linha reta. Este exemplo utiliza a regressão linear simples, onde o quadrado da distância entre a linha vermelha e cada ponto de amostra é minimizado.
Utilização
Economia
A regressão linear é a principal ferramenta analítica em economia. Por exemplo, ela é usada para adivinhar gastos de consumo, gastos com investimentos fixos, investimentos em estoques, compras de exportações de um país, gastos com importações, a demanda para manter ativos líquidos, a demanda de mão-de-obra e a oferta de mão-de-obra.
Perguntas e Respostas
P: O que é regressão linear?
R: Regressão linear é uma maneira de ver como algo muda quando outras coisas mudam, usando a matemática. Ela usa uma variável dependente e uma ou mais variáveis explicativas para criar uma linha reta, conhecida como a "linha de regressão".
P: Quais são as vantagens da regressão linear?
R: Os modelos que dependem linearmente de seus parâmetros desconhecidos são mais fáceis de encaixar do que os modelos que não estão relacionados linearmente com seus parâmetros. Além disso, as propriedades estatísticas dos estimadores resultantes são mais fáceis de determinar.
P: Quais são alguns usos práticos para a regressão linear?
R: A regressão linear pode ser usada para ajustar um modelo de previsão aos valores (dados) observados, a fim de fazer previsões, previsões ou reduções. Ela também pode ser usada para quantificar a força das relações entre variáveis e identificar subconjuntos de dados que contenham informações redundantes sobre outra variável.
P: Como os modelos de regressão linear tentam minimizar os erros?
R: Modelos de regressão linear tentam fazer com que a distância vertical entre a linha e os pontos de dados (os resíduos) seja a menor possível. Isso é feito minimizando ou a soma dos quadrados dos residuais (menos quadrados), a falta de ajuste em alguma outra norma (menos desvios absolutos), ou minimizando uma versão penalizada da função de perda dos mínimos quadrados (regressão de cristas).
P: É possível que os modelos de regressão linear não se baseiem nos mínimos quadrados?
R: Sim, é possível que modelos de regressões lineares não se baseiem em mínimos quadrados, mas usem métodos tais como minimizar a falta de ajuste em alguma outra norma (menos desvios absolutos) ou minimizar uma versão penalizada da função de perda de menos quadrados (regressão de cristas).
P: São sinônimos de "modelo linear" e "mínimos quadrados"?
R: Não, eles não são sinônimos. Enquanto eles estão intimamente ligados, "modelo linear" se refere especificamente ao uso de uma linha reta, enquanto "mínimos quadrados" se refere especificamente à tentativa de minimizar erros, assegurando que haja uma distância vertical mínima entre a linha e os pontos de dados.
Pesquise na enciclopédia