Equação Young-Laplace
Em física, a equação Young-Laplace (/ləˈplɑːs/) é uma equação diferencial parcial não linear que descreve a diferença de pressão capilar através da interface entre dois fluidos estáticos, tais como água e ar. Esta diferença é devida ao fenômeno de tensão superficial ou tensão de parede. A tensão de parede só pode ser usada para paredes muito finas. A equação Young-Laplace relaciona a diferença de pressão com a forma da superfície ou da parede. Ela é muito importante no estudo de superfícies capilares estáticas.
Em fisiologia, é conhecida como a lei de Laplace. É usada para descrever a pressão dentro de órgãos ocos.
A equação tem o nome de Thomas Young, que desenvolveu a teoria qualitativa da tensão superficial em 1805, e Pierre-Simon Laplace, que completou a descrição matemática no ano seguinte. Às vezes também é chamada de equação Young-Laplace-Gauss: Carl Friedrich Gauss unificou o trabalho de Young e Laplace em 1830. Gauss derivou tanto a equação diferencial quanto as condições de fronteira usando os princípios de trabalho virtual de Johann Bernoulli.
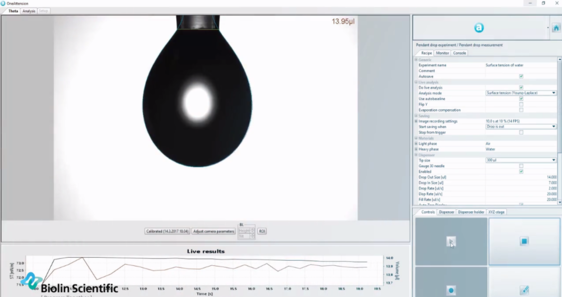
Os tensiômetros ópticos utilizam a equação Young-Laplace para determinar a tensão superficial do líquido automaticamente com base na forma de gotas pendentes.
