Função Heaviside

A função Heaviside, H, é uma função não contínua cujo valor é zero para uma entrada negativa e um para uma entrada positiva.

A função é utilizada na teoria matemática do controle para representar um sinal que se liga em um determinado momento e permanece ligado indefinidamente. Foi nomeado em homenagem ao inglês Oliver Heaviside.

A função Heaviside é a parte integrante da função Dirac delta: H′ = δ. Isto às vezes é escrito como

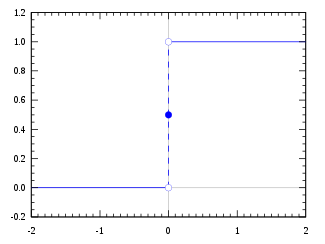
A função de degrau Heaviside, utilizando a convenção do meio-máximo

Forma discreta

Também podemos definir uma forma alternativa da função passo a passo Heaviside como uma função de uma variável discreta, n:

H [ n ] = { 0 , n < 0 1 , n ≥ 0 {\i1}displaystyle H[n]={\i1}begin{\i}0,&n<0,&n<0,1,&ngeq 0{\i}end{\i} $H[n]={\begin{cases}0,&n<0\\1,&n\geq 0\end{cases}}$

onde n é um número inteiro.

H ( x ) = lim z → x - ( ( | z | / z + 1 ) / 2 ) {\displaystyle H(x)=\lim _{z\rightarrow x^{-}}((|z|/z+1)/2)} $H(x)=\lim _{z\rightarrow x^{-}}((|z|/z+1)/2)$

O impulso da unidade de tempo discreto é a primeira diferença da etapa de tempo discreto

δ [ n ] = H [ n ] - H [ n - 1 ] . estilo de jogo {\delta {\delta esquerda[n] -H[n] -H[n-1]. } $\delta \left[n\right]=H[n]-H[n-1].$

Esta função é a soma cumulativa do delta do Kronecker:

H [ n ] = ∑ k = - ∞ n δ δ [ k ] {\i1}displaystyle H[n]=sum _{k=-->infty }^{n}delta [k]},} $H[n]=\sum _{k=-\infty }^{n}\delta [k]\,$

onde

δ [ k ] = δ k , 0 {\i1}displaystyle {\i}delta [k]=delta _{k,0},} $\delta [k]=\delta _{k,0}\,$

é a função de impulso da unidade discreta.

Representações

Muitas vezes é útil uma representação integral da função de passos da Heaviside:

H ( x ) = lim ϵ → 0 + - 1 2 π i ∫ - ∞ ∞ 1 τ + i ϵ e - i x τ d τ = lim ϵ → 0 + 1 2 π i ∫ - ∞ ∞ ∞ 1 τ - i ϵ e i x τ d τ . H(x)=lim _epsilon ^{+}-{1 {1 {\i}- acima de 2\i {i} em grande parte... em grande parte... \epsilon x^mathrm \tau =lim _epsilon 0 ^{+}{1 acima de 2 ^pi ^mathrm {i} em grande quantidade... \epsilon Mathrm \tau . } $H(x)=\lim _{\epsilon \to 0^{+}}-{1 \over 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \over \tau +\mathrm {i} \epsilon }\mathrm {e} ^{-\mathrm {i} x\tau }\mathrm {d} \tau =\lim _{\epsilon \to 0^{+}}{1 \over 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \over \tau -\mathrm {i} \epsilon }\mathrm {e} ^{\mathrm {i} x\tau }\mathrm {d} \tau .$

H(0)

O valor da função a 0 pode ser definido como H(0) = 0, H(0) = ½ ou H(0) = 1.

H ( x ) = 1 + sgn ( x ) 2 = { 0 , x < 0 1 2 , x = 0 1 , x > 0. {\displaystyle H(x)={\frac {1+\operatorname {sgn}(x)}{2}}={\begin{cases}0,&x<0\\{\frac {1}{2}},&x=0\\1,&x>0.\end{cases}}} $H(x)={\frac {1+\operatorname {sgn}(x)}{2}}={\begin{cases}0,&x<0\\{\frac {1}{2}},&x=0\\1,&x>0.\end{cases}}$

Páginas relacionadas

Transformar Laplace

Perguntas e Respostas

P: O que é a função Heaviside?

R: A função Heaviside é uma função não contínua cujo valor é zero para uma entrada negativa e um para uma entrada positiva.

P: Por que a função Heaviside é usada na teoria de controle?

R: A função Heaviside é usada na teoria de controle para representar um sinal que é ligado em um momento específico e permanece ligado indefinidamente.

P: Quem é a pessoa que deu nome à função Heaviside?

R: A função Heaviside recebeu esse nome em homenagem ao inglês Oliver Heaviside.

P: Qual é a relação entre a função Heaviside e a função delta de Dirac?

R: A função de Heaviside é a integral da função delta de Dirac: H′(x)= δ(x).

P: Qual é a saída da função Heaviside para entradas positivas?

R: A função Heaviside produz um para entradas positivas.

P: Qual é a saída da função Heaviside para entradas negativas?

R: A função Heaviside produz zero para entradas negativas.

P: Que tipo de função é a função Heaviside?

R: A função Heaviside é uma função não contínua.