Espaço de probabilidade
O espaço de probabilidade é um modelo matemático utilizado para descrever experimentos científicos Um espaço de probabilidade consiste em três partes:
- Um espaço de amostra que lista todos os resultados possíveis
- Um conjunto de eventos. Cada evento associa zero ou mais resultados
- Uma função que atribui probabilidades a cada evento
Um resultado é o resultado de uma única execução do modelo. Como os resultados individuais podem ser de pouca utilidade prática, eventos mais complexos são usados para caracterizar grupos de resultados. A coleção de todos esses eventos é um estilo de escrita ao estilo σ-algebra F 
. Finalmente, há a necessidade de especificar a probabilidade de cada evento acontecer. Isto é feito usando a função de medida de probabilidade, P.
Uma vez estabelecido o espaço de probabilidade, assume-se que a "natureza" faz seu movimento e seleciona um único resultado, ω, a partir do espaço de amostra Ω. Todos os eventos no estilo F {\i1}escrito em estilo F {\i1} que contêm o resultado selecionado ω (lembre-se que cada evento é um subconjunto de Ω) são ditos como "ocorreram". A seleção realizada por natureza é feita de tal forma que se o experimento fosse repetido um número infinito de vezes, as freqüências relativas de ocorrência de cada um dos eventos coincidiriam com as probabilidades prescritas pela função P.
O proeminente matemático soviético Andrey Kolmogorov introduziu a noção de espaço de probabilidade, juntamente com outros axiomas de probabilidade, na década de 1930.
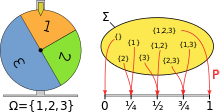
Modelagem de uma roda da fortuna utilizando o espaço de probabilidade
Perguntas e Respostas
P: O que é um espaço de probabilidade?
R: Um espaço de probabilidade é um modelo matemático usado para descrever experimentos científicos. Ele consiste de três partes: um espaço de amostra que lista todos os resultados possíveis, um conjunto de eventos que associam zero ou mais resultados, e uma função que atribui probabilidades a cada evento.
P: Em que consiste o espaço de amostra?
R: O espaço de amostragem consiste de todos os resultados possíveis, muitas vezes escritos como Ω {\displaystyle \Omega }. e um resultado como ω .
P: O que é um resultado?
R: Um resultado é o resultado de uma única execução do modelo.
P: Para que servem os eventos nos espaços de probabilidade?
R: Os eventos são usados para caracterizar grupos de resultados, já que resultados individuais podem ser de pouca utilidade prática. A coleção de todos esses eventos é chamada de álgebra σ, às vezes escrita como F {\fisplaystyle {\mathcal {\f}} .
P: Como as probabilidades são atribuídas a cada evento?
R: As probabilidades são atribuídas a cada evento usando a função de medida de probabilidade P.
P: Quem introduziu a noção de espaços de probabilidade? R: O proeminente matemático soviético Andrey Kolmogorov introduziu a noção de espaços de probabilidade juntamente com outros axiomas de probabilidade na década de 1930.
