Postulado paralelo
Em geometria, o postulado paralelo é um dos axiomas da geometria euclidiana. Às vezes também é chamado de quinto postulado de Euclides, porque é o quinto postulado nos Elementos de Euclides.
O postulado diz isso:
Se você cortar um segmento de linha com duas linhas, e os dois ângulos interiores que as linhas formam somam menos de 180°, então as duas linhas eventualmente se encontrarão se você as estender por tempo suficiente.
O campo da geometria que segue todos os axiomas de Euclides é chamado de geometria euclidiana. Geometrias que não seguem todos os axiomas de Euclides são chamadas de geometria não euclidiana.
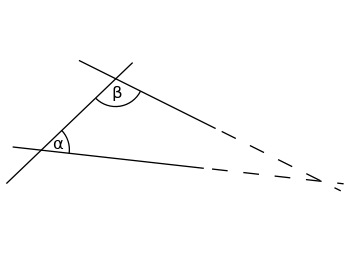
Se a soma dos ângulos internos α (alfa) e β (beta) for inferior a 180°, as duas linhas se cruzarão em algum lugar, se ambas forem prolongadas até o infinito.
História
Alguns matemáticos pensavam que o quinto postulado de Euclides era muito mais longo e complicado do que os outros quatro postulados. Muitos deles pensavam que isso poderia ser comprovado a partir dos outros axiomas mais simples. Alguns matemáticos anunciaram que haviam provado a proposição a partir das proposições mais simples, mas todos eles acabaram se equivocando.
O axioma da feira de jogos
Outra proposta mais recente conhecida como o axioma da Playfair é semelhante ao quinto postulado de Euclides. Diz o axioma:
Dada uma linha reta e um ponto não nesta linha, você só pode traçar uma linha reta através deste ponto que não irá encontrar a outra linha reta.
Na verdade, os matemáticos descobriram que este axioma não só é semelhante ao quinto postulado de Euclides, mas tem exatamente as mesmas implicações. Matematicamente, as duas proposições são chamadas de proposições 'equivalentes'. Hoje, o axioma da Playfair é utilizado com mais freqüência pelos matemáticos do que o postulado paralelo original de Euclid.
Geometria não-euclidiana
Eventualmente, alguns matemáticos tentaram construir novas geometrias sem utilizar o axioma. Um tipo de geometria não euclidiana é chamada de geometria elíptica. Na geometria elíptica, o postulado paralelo é substituído por um axioma que afirma isso:
Dada uma linha reta e um ponto não nesta linha, não se pode traçar uma linha reta através deste ponto que eventualmente não cruzará a outra linha reta.
Os matemáticos descobriram que quando substituíram o quinto postulado de Euclides por este axioma, eles ainda conseguiram provar muitos dos outros teoremas de Euclides. Uma maneira de imaginar a geometria elíptica é pensando na superfície de um globo terrestre. Em um globo, as linhas de longitude parecem ser paralelas no equador, mas todas elas se encontram nos pólos. No final do século XIX, a geometria elíptica mostrou-se consistente. Isto provou que o quinto postulado de Euclides não era independente dos outros postulados. Depois disso, a maioria dos matemáticos deixou de tentar provar o quinto postulado dos outros quatro postulados. Ao invés disso, muitos matemáticos começaram a estudar outras geometrias que não seguem o quinto postulado de Euclides.
Outros matemáticos axiomáticos às vezes substituem o quinto axioma de Euclides por dizer isso:
Dada uma linha reta e um ponto não nesta linha, você pode traçar pelo menos duas linhas retas através deste ponto que eventualmente não cruzará a outra linha reta.
Isto é chamado de geometria hiperbólica.
Outra geometria simplesmente remove o quinto postulado de Euclides e não o substitui por nada. Isto é chamado de geometria neutra ou geometria absoluta.
Pesquise na enciclopédia