Função de densidade de probabilidade

Uma função de densidade de probabilidade é uma função que pode ser definida para qualquer distribuição de probabilidade contínua. A integral da função de densidade de probabilidade no intervalo [ a , b ] {\ a , b ] $[a,b]$ produz a probabilidade de que uma dada variável aleatória com a densidade dada esteja contida no intervalo fornecido.

A função de densidade de probabilidade é necessária para poder trabalhar com distribuições contínuas. Lançar um dado dará os números de 1 a 6, com uma probabilidade de 1 6 {\frac {1}{6}}}. ${\tfrac {1}{6}}$ mas esta não é uma função contínua, pois apenas os números 1 a 6 são possíveis. Em contraste, duas pessoas não terão a mesma altura, ou o mesmo peso. Usando uma função de densidade de probabilidade, é possível determinar a probabilidade para pessoas entre 180 centímetros (71 pol) e 181 centímetros (71 pol), ou entre 80 quilogramas (176,4 lb) e 81 quilogramas (178,6 lb), embora existam infinitamente muitos valores entre estes dois limites.

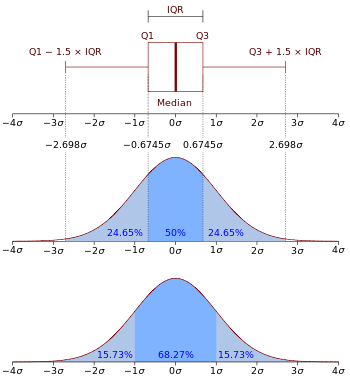
Boxplot e função de densidade de probabilidade de uma distribuição normal N(0, σ2) .

Perguntas e Respostas

P: O que é uma função de densidade de probabilidade?

R: Uma função de densidade de probabilidade é uma função que caracteriza qualquer distribuição de probabilidade contínua.

P: Como é escrita a função de densidade de probabilidade de uma variável aleatória X?

R: A função de densidade de probabilidade de X é por vezes escrita como f_X(x).

P: O que representa a integral da função de densidade de probabilidade?

R: O integral da função de densidade de probabilidade representa a probabilidade de uma dada variável aleatória com a densidade dada estar contida num intervalo fornecido.

P: A função de densidade de probabilidade é sempre não-negativa em todo o seu domínio?

R: Sim, por definição, a função de densidade de probabilidade é não-negativa em todo o seu domínio.

P: A integração num intervalo totaliza até 1?

R: Sim, a integração num intervalo totaliza até 1.

P: Que tipo de distribuição caracteriza uma Função de Densidade de Probabilidade?

R: Uma Função de Densidade de Probabilidade caracteriza qualquer distribuição de probabilidade contínua.