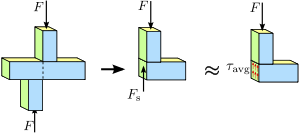Estresse (mecânica)
O estresse é a força por unidade de área em um corpo que tende a fazer com que ele mude de forma.
O estresse é uma medida das forças internas de um corpo entre suas partículas. Essas forças internas são uma reação às forças externas aplicadas sobre o corpo que o fazem se separar, comprimir ou deslizar. As forças externas são forças de superfície ou forças do corpo. Tensão é a força média por unidade de área que uma partícula de um corpo exerce sobre uma partícula adjacente, através de uma superfície imaginária que as separa.
A fórmula para a tensão normal uniaxial é:
σ = F A {\frac {\frac {\frac {\frac {\frac {\frac {\frac }}}
onde σ é o estresse, F é a força e A é a área de superfície.
Nas unidades SI, a força é medida em newtons e a área em metros quadrados. Isto significa que a tensão é newtons por metro quadrado, ou N/m2. No entanto, a tensão tem sua própria unidade SI, chamada de pascal. 1 pascal (símbolo Pa) é igual a 1 N/m2. Em unidades Imperial, a tensão é medida em libra-força por polegada quadrada, que muitas vezes é encurtada para "psi". A dimensão da tensão é a mesma que a da pressão.
Na mecânica contínua, o corpo deformável carregado comporta-se como um corpo contínuo. Portanto, estas forças internas são distribuídas continuamente dentro do volume do corpo material. (Isto significa que a distribuição de tensão no corpo é expressa como uma função de espaço e tempo em forma contínua). As forças causam deformação da forma do corpo. A deformação pode levar a uma mudança de forma permanente ou falha estrutural se o material não for suficientemente forte.
Alguns modelos de mecânica contínua tratam a força como algo que pode mudar. Outros modelos olham para a deformação da matéria e dos corpos sólidos, porque as características da matéria e dos sólidos são tridimensionais. Cada abordagem pode dar resultados diferentes. Modelos clássicos de mecânica contínua assumem uma força média e não incluem adequadamente "fatores geométricos". (A geometria do corpo pode ser importante para a forma como o estresse é compartilhado e como a energia se acumula durante a aplicação da força externa).
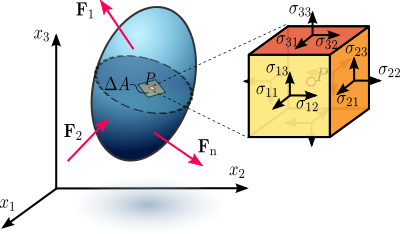
Figura 1.1 Tensão em um corpo de material deformável carregado assumido como um continuum.
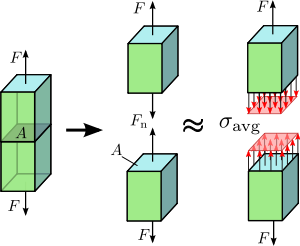
Figura 1.2 Tensão axial em uma barra prismática carregada axialmente.
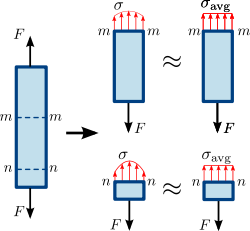
Figura 1.3 Tensão normal em uma barra prismática (membro reto de seção transversal uniforme). A distribuição de tensão ou força na seção transversal da barra não é necessariamente uniforme. No entanto, uma tensão normal média σ a v g {\i1}displaystyle {\i}sigma _{\i}mathrm }\,\! 
Figura 1.4 Tensão de cisalhamento em uma barra prismática. A distribuição de tensão ou força na seção transversal da barra não é necessariamente uniforme. No entanto, uma tensão de cisalhamento média τ a v g {\i1}displaystyle {\i}tau _{\i1}mathrm }\,\! 
Tensão de cisalhamento
Mais informações: Tensão de cisalhamento
Tensões simples
Em algumas situações, a tensão dentro de um objeto pode ser descrita por um único número, ou por um único vetor (um número e uma direção). Três situações de tensão tão simples são a tensão normal uniaxial, a tensão de cisalhamento simples e a tensão normal isotrópica.
Tensão normal uniaxial
Tensão de tração (ou tensão) é o estado de tensão que leva à expansão; ou seja, o comprimento de um material tende a aumentar na direção da tração. O volume do material permanece constante. Quando forças iguais e opostas são aplicadas sobre um corpo, então a tensão devida a esta força é chamada de tensão de tração.
Portanto, em um material uniaxial, o comprimento aumenta na direção da tensão de tração e as outras duas direções diminuirão de tamanho. Na forma uniaxial de tensão, a tensão de tração é induzida por forças de tração. A tensão de tração é o oposto da tensãocompressiva.
Os membros estruturais em tensão direta são cordas, âncoras e pregos do solo, parafusos, etc. As vigas sujeitas a momentos de flexão podem incluir tensão de tração, bem como tensão de compressão e/ou tensão de cisalhamento.
A tensão de tração pode ser aumentada até o alcance da resistência à tração, ou seja, o estado limite de tensão.
Tensão em corpos unidimensionais
Todos os objetos reais ocupam um espaço tridimensional. Entretanto, se duas dimensões forem muito grandes ou muito pequenas em comparação com as outras, o objeto pode ser modelado como unidimensional. Isto simplifica a modelagem matemática do objeto. Os objetos unidimensionais incluem um pedaço de arame carregado nas extremidades e visto de lado, e uma chapa metálica carregada na face e vista de perto e através da seção transversal.
Páginas relacionadas
- Tensão
- Dobragem
Perguntas e Respostas
P: O que é estresse?
R: O estresse é a força por unidade de área em um corpo que tende a fazer com que ele mude de forma. É uma medida das forças internas de um corpo entre suas partículas, e é a força média por unidade de área que uma partícula de um corpo exerce sobre uma partícula adjacente através de uma superfície imaginária que as separa.
P: Como é que as forças externas afetam o estresse?
R: Forças externas são forças de superfície ou forças do corpo, e causam deformação da forma do corpo que pode levar à mudança permanente da forma ou falha estrutural se o material não for suficientemente forte.
P: Qual é a fórmula para a tensão normal uniaxial?
R: A fórmula para a tensão normal uniaxial é σ = F/A, onde σ é a tensão, F é a força e A é a área da superfície. Em unidades SI, a força é medida em newtons e a área em metros quadrados, o que significa que a tensão seria newtons por metro quadrado (N/m2). No entanto, existe sua própria unidade SI para tensão chamada pascal (Pa), que equivale a 1 N/m2. Em unidades Imperial, ela seria medida em libra-força por polegada quadrada (psi).
P: O que a mecânica do contínuo assume sobre a força?
R: Modelos clássicos da mecânica do contínuo assumem uma força média e não incluem adequadamente fatores geométricos - o que significa que eles não levam em conta como a geometria afeta como a energia se acumula durante a aplicação da força externa.
P: Como diferentes modelos podem dar resultados diferentes quando se observa a deformação da matéria e dos corpos sólidos?
R: Modelos diferentes olham para a deformação da matéria e dos corpos sólidos de maneira diferente porque as características da matéria e dos sólidos são tridimensionais - assim cada abordagem leva em conta aspectos diferentes que podem levar a resultados diferentes.
P: Como a mecânica contínua trata os corpos deformáveis carregados?
R: A mecânica contínua trata os corpos deformáveis carregados como contínuos - o que significa que as forças internas são distribuídas continuamente dentro do volume do corpo material, em vez de serem concentradas em certos pontos, como nos modelos clássicos.
Pesquise na enciclopédia