Cilindro
Um cilindro é uma das formas geométricas curvas mais básicas, com a superfície formada pelos pontos a uma distância fixa de um determinado segmento de linha, conhecido como o eixo do cilindro. A forma pode ser pensada como um prisma circular. Tanto a superfície quanto a forma sólida criada no interior podem ser chamadas de cilindro. A área da superfície e o volume de um cilindro são conhecidos desde os tempos antigos.
Na geometria diferencial, um cilindro é definido mais amplamente como qualquer superfície governada que é abrangida por uma família de um parâmetro de linhas paralelas. Um cilindro cuja seção transversal é uma elipse, parábola ou hipérbole é chamado de cilindro elíptico, cilindro parabólico ou cilindro hiperbólico respectivamente.
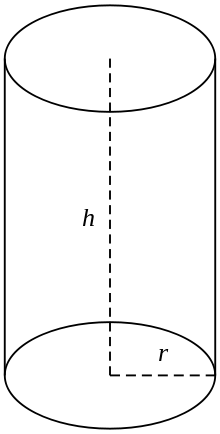
Um cilindro circular direito
Uso comum
Em uso comum, entende-se por cilindro uma seção finita de um cilindro circular direito, ou seja, o cilindro com as linhas geradoras perpendiculares às bases, com suas extremidades fechadas para formar duas superfícies circulares, como na figura (à direita). Se o cilindro tem um raio r e comprimento (altura) h, então seu volume é dado por:
V = πr2h
e sua área de superfície é:
- a área do topo (πr2) +
- a área do fundo (πr2) +
- a área da lateral (2πrh).
Portanto, sem a parte superior ou inferior (área lateral), a área de superfície é:
A = 2πrh.
Com a parte superior e inferior, a área de superfície é:
A = 2πr2 + 2πrh = 2πr(r + h).
Para um determinado volume, o cilindro com a menor área de superfície tem h = 2r. Para uma determinada área de superfície, o cilindro com o maior volume tem h = 2r, ou seja, o cilindro cabe em um cubo (altura = diâmetro).
Volume
Tendo um cilindro circular direito com uma altura h unidades e uma base de raio r unidades com os eixos coordenados escolhidos de modo que a origem esteja no centro de uma base e a altura seja medida ao longo do eixo positivo x. Uma seção plana a uma distância de x unidades da origem tem uma área de A(x) unidades quadradas onde
A ( x ) = π r 2 {\\i1}displaystyle A(x)==pi r^{\i}}
ou
A ( y ) = π r 2 {\i1}displaystyle A(y)==pi r^{2}}
Um elemento de volume, é um cilindro direito de área de base unidades quadradas de Awi e uma espessura de Δix unidades. Assim, se V unidades cúbicas é o volume do cilindro circular direito, por soma de Riemann,
V o l u m e o d e c y l i n d e r = lim | Δ → 0 | | ∑ i = 1 n A ( w i ) Δ i x {\i}displaystyle {\i} {\i1}mathrm {\i} =lim _{\i=1}{\i=1}A(w_{\i}){\i}Delta _{\i}x
= ∫ 0 h A ( y ) 2 d y {\i1}displaystyle =int _{0}^{h}A(y)^{2},dy}
= ∫ 0 h π r 2 d y {\i1}displaystyle =int _{0}^{h}pi r^{2},dy}
= π r 2 h {\i1}displaystyle ==,r^{2},h,}
Usando coordenadas cilíndricas, o volume pode ser calculado por integração sobre
= ∫ 0 h ∫ 0 2 π ∫ 0 r s d s d ϕ d z {\i1}displaystyle =int _{0}^^^^^^^^ 2pi ^int _{0}^s,^,ds,dz}
= π r 2 h {\i1}displaystyle ==,r^{2},h,}
Seção cilíndrica
As seções cilíndricas são as interseções dos cilindros com os planos. Para um cilindro circular direito, há quatro possibilidades. Um plano tangente ao cilindro, encontra o cilindro em uma única linha reta. Movido paralelamente a si mesmo, o plano ou não intercepta o cilindro ou o intercepta em duas linhas paralelas. Todos os outros planos cruzam o cilindro em uma elipse ou, quando estão perpendiculares ao eixo do cilindro, em um círculo.
Outros tipos de cilindros
Um cilindro elíptico, ou cilíndroide, é uma superfície quadriculada, com a seguinte equação em coordenadas cartesianas:
( x a ) 2 + ( y b ) 2 = 1. Estilo de jogo Esquerda(x a ) 2 + Esquerda(x b ) 2 = 1.
Esta equação é para um cilindro elíptico, uma generalização do cilindro comum, circular (a = b). Ainda mais geral é o cilindro generalizado: a seção transversal pode ser qualquer curva.
O cilindro é um quadriculado degenerado porque pelo menos uma das coordenadas (neste caso z) não aparece na equação.
Um cilindro oblíquo tem as superfícies superior e inferior deslocadas uma da outra.
Existem outros tipos de cilindros mais incomuns. Estes são os cilindros elípticos imaginários:
2 + ( x a ) 2 + ( y b ) 2 = - 1 Estilo de exibição Esquerda(x a )
o cilindro hiperbólico:
2 - ( x a ) 2 - ( y b ) 2 = 1 Estilo de exibição Esquerda(x a ) Direita(2) - Esquerda(2) - Esquerda(2) - Esquerda(3) - Direita(4)
e o cilindro parabólico:
x 2 + 2 a y = 0. ^{\\i1}- estilo de jogo x^{\i}+2ay=0,^,}

Um cilindro elíptico

Na geometria projetiva, um cilindro é simplesmente um cone cujo ápice está no infinito, que corresponde visualmente a um cilindro em perspectiva parecendo ser um cone em direção ao céu.
Geometria projetiva
Em geometria projetiva, um cilindro é simplesmente um cone cujo ápice está no infinito.
Isto é útil na definição de cónicas degeneradas, que requerem a consideração das cónicas cilíndricas.
Perguntas e Respostas
P: O que é um cilindro?
R: Um cilindro é uma forma geométrica tridimensional com a superfície formada por pontos a uma distância fixa de um determinado segmento de linha, conhecido como o eixo do cilindro. Pode ser pensado como um prisma circular e tanto a superfície quanto a forma sólida criada no interior podem ser chamadas de cilindro.
P: Há quanto tempo as pessoas sabem sobre a área da superfície e o volume dos cilindros?
R: A área da superfície e o volume dos cilindros são conhecidos desde os tempos antigos.
P: O que são cilindros elípticos, parabólicos e hiperbólicos?
R: Cilindros elípticos, parabólicos e hiperbólicos são cilindros cuja seção transversal é uma elipse, parábola ou hipérbole, respectivamente.
P: Como é definido um cilindro em geometria diferencial?
R: Em geometria diferencial, um cilindro é definido mais amplamente como uma superfície governada que é compreendida por uma família de um parâmetro de linhas paralelas.
P: O que significa para algo ser "governado"?
R: Ser "governado" significa que ele tem linhas retas desenhadas de uma maneira ou de outra.
P: Existe apenas um tipo de cilindro?
R: Não, há muitos tipos diferentes de cilindros, tais como cilindros elípticos, parabólicos e hiperbólicos, todos com seções transversais diferentes.
Pesquise na enciclopédia










