Círculo
Um círculo é uma forma redonda, bidimensional. Todos os pontos na borda do círculo estão à mesma distância do centro.
O raio de um círculo é uma linha do centro do círculo até um ponto ao lado. Os matemáticos utilizam a letra r para o comprimento do raio de uma circunferência. O centro de uma circunferência é o ponto bem no meio.
O diâmetro (que significa "todo o caminho transversal") de um círculo é uma linha reta que vai de um lado para o oposto e atravessa o centro do círculo. Os matemáticos utilizam a letra d para o comprimento desta linha. O diâmetro de uma circunferência é igual ao dobro de seu raio (d é igual a 2 vezes r).
d = 2 r {\displaystyle d=2\r}
A circunferência (que significa "em toda a volta") de um círculo é a linha que contorna o centro do círculo. Os matemáticos usam a letra C para o comprimento desta linha.
O número π (escrito como a letra grega pi) é um número muito útil. É o comprimento da circunferência dividido pelo comprimento do diâmetro (π é igual a C dividido por d). Como fração, o número π é igual a cerca de 22⁄7 ou 335/113 (que é mais próximo) e como número é cerca de 3,1415926535.
A área, a, dentro de um círculo é igual ao raio multiplicado por si mesmo, depois multiplicado por π (um igual a π vezes r vezes r).

Um círculo
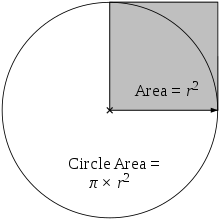
A área do círculo é igual a π vezes a área do quadrado cinza.
Calculando π
π pode ser medida desenhando um círculo grande, depois medindo seu diâmetro (d) e circunferência (C). Isto porque a circunferência de um círculo é sempre π vezes seu diâmetro.
π = C d d {\i1}displaystyle {\i} ={\i1}frac {\i}{\i}
π também pode ser calculado usando apenas métodos matemáticos. A maioria dos métodos usados para calcular o valor de π tem propriedades matemáticas desejáveis. Entretanto, eles são difíceis de entender sem conhecer trigonometria e cálculo. Entretanto, alguns métodos são bastante simples, como esta forma da série Gregory-Leibniz:
π = 4 1 - 4 3 + 4 5 - 4 7 + 4 9 - 4 11 ⋯ ⋯ {\i1}-{\i1}-{\i1}-{\i1}frac {\i}-{\i1}- 4 4 4}{\i}- 5-{\i1}-{\i1}- 4 4 4}- 4 4 4}- 4 4 4= 4
Embora essa série seja fácil de escrever e calcular, não é fácil ver por que é igual a π. Uma abordagem mais fácil de entender é desenhar um círculo imaginário de raio r centrado na origem. Então qualquer ponto (x,y) cuja distância d da origem seja menor que r, calculada pelo teorema de pitágoras, estará dentro do círculo:
d = x 2 + y 2 {\i1}displaystyle d={\i}{x^{2}+y^{2}}}}
Encontrar um conjunto de pontos dentro do círculo permite estimar a área A do círculo. Por exemplo, usando coordenadas inteiras para um grande r. Como a área A de um círculo é π vezes o raio ao quadrado, π pode ser aproximado usando:
π = A r 2 {\i} {r^{2}}}}
Páginas relacionadas
- Esfera
Perguntas e Respostas
P: O que é um círculo?
R: Um círculo é uma forma redonda, bidimensional. Todos os pontos na borda do círculo estão à mesma distância do centro.
P: O que os matemáticos usam para representar o comprimento do raio de um círculo?
R: Os matemáticos usam a letra r para representar o comprimento do raio de um círculo.
P: O que está escrito como O em círculos?
R: O centro de um círculo é freqüentemente escrito como O.
P: Qual é o comprimento do diâmetro de um círculo?
R: O diâmetro (que significa "até o centro") de um círculo é uma linha reta que vai de um lado para o oposto e passa pelo centro do círculo. É igual ao dobro de seu raio (d é igual a 2 vezes r).
P: Que letra os matemáticos usam para representar a circunferência?
R: Os matemáticos usam C para a circunferência, que significa "ao redor".
P: Como podemos calcular a área dentro de um círculo?
R: A área, R, dentro de um círculo pode ser calculada multiplicando-se seu raio por si mesma e depois multiplicando-se por ً (R igual a ً vezes r vezes r).
Pesquise na enciclopédia




