Pi

Aproximação

Pi é freqüentemente escrito formalmente como π ou a carta grega π como um atalho. Pi também é um número irracional, significando que não pode ser escrito como uma fração ( a b {\displaystyle a {\displaystyle a \displaystyle b} ), onde 'a' e 'b' são números inteiros (números inteiros). Isto significa basicamente que os dígitos de pi que estão à direita do decimal vão para sempre sem se repetir em um padrão, e que é impossível escrever o valor exato de pi como um número. Pi só pode ser aproximado, ou medido a um valor que seja suficientemente próximo para fins práticos.

Um valor próximo a pi é 3,141592653589793238462643... Uma fração comum aproximada de pi é 22 7 {\displaystyle 22 acima de 7} que rende aproximadamente 3.14285714. Esta aproximação está a 0,04% do valor real do pi. Enquanto esta aproximação é aceita para a maior parte de seu uso na vida real, a fração 355 113 {\displaystyle 355 {\displaystyle 355 acima de 113} é mais precisa (dando cerca de 3,14159292), e pode ser usada quando um valor mais próximo de pi é necessário. Os computadores podem ser usados para obter melhores aproximações de pi.

Em março de 2019, Emma Haruka Iwao calculou o valor de pi para 31,4 trilhões de dígitos.

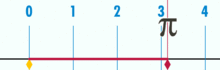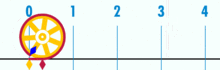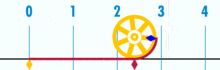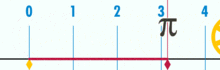
Um diagrama mostrando como π pode ser encontrado usando um círculo com um diâmetro de um. A circunferência deste círculo é π.

História

O valor do pi era conhecido por matemáticos indianos antigos como Bhaskaracharya e Aryabhatta.

Os matemáticos conhecem o pi há milhares de anos porque trabalham com círculos há o mesmo tempo. Civilizações tão antigas quanto os babilônios têm sido capazes de aproximar pi a muitos dígitos, como a fração 25/8 e 256/81. A maioria dos historiadores acredita que os antigos egípcios não tinham o conceito de π e que a correspondência é uma coincidência.

A primeira referência escrita a pi data de 1900 AC. Por volta de 1650 AC, os Ahmes egípcios deram um valor no Rhind Papyrus. Os babilônios conseguiram descobrir que o valor de pi era ligeiramente maior do que 3, simplesmente fazendo um grande círculo e depois colando um pedaço de corda na circunferência e no diâmetro, anotando suas distâncias, e depois dividindo a circunferência pelo diâmetro.

O conhecimento do número pi passou de volta para a Europa e para as mãos dos hebreus, que tornaram o número importante em uma seção da Bíblia chamada Velho Testamento. Depois disso, a maneira mais comum de tentar encontrar pi era desenhar uma forma de muitos lados dentro de qualquer círculo e usar a área da forma para encontrar pi. O filósofo grego Arquimedes, por exemplo, usou uma forma de polígono que tinha 96 lados para encontrar o valor de pi, mas os chineses em 500 CE conseguiram usar um polígono com 16.384 lados para encontrar o valor de pi. Os gregos, como Anaxágoras de Clazomenae, também estavam ocupados em descobrir outras propriedades do círculo, como por exemplo, como fazer quadrados de círculos e esquadriar o número pi. Desde então, muitas pessoas têm tentado descobrir mais e mais valores exatos de pi.

Uma história de pi
Filósofo	Data	Aproximação
Claudius Ptolomeu	cerca de 150 CE	3.1416
Zu Chongzhi	430-501 CE	3.1415929203
al-Khwarizmi	cerca de 800 CE	3.1416
al-Kashi	por volta de 1430	3.14159265358979
Viète	1540–1603	3.141592654
Roomen	1561–1615	3.14159265358979323
Van Ceulen	por volta de 1600	3.14159265358979323846264338327950288

No século 16, melhores e melhores maneiras de encontrar pi se tornaram disponíveis, como a fórmula complicada que o advogado francês François Viète desenvolveu. O primeiro uso do símbolo grego "π" foi em um ensaio escrito em 1706 por William Jones.

Um matemático chamado Lambert também mostrou em 1761 que o número pi era irracional; ou seja, não pode ser escrito como uma fração pelos padrões normais. Outro matemático chamado Lindeman também foi capaz de mostrar em 1882 que pi fazia parte do grupo de números conhecidos como transcendentais, que são números que não podem ser a solução para uma equação polinomial.

Pi também pode ser usado para descobrir muitas outras coisas ao lado de círculos. As propriedades do pi permitiram que ele fosse usado em muitas outras áreas da matemática além da geometria, que estuda formas. Algumas dessas áreas são análises complexas, trigonometria e séries.

Pi na vida real

Hoje, existem diferentes maneiras de calcular muitos dígitos de π. No entanto, isto é de utilidade limitada.

Pi pode às vezes ser usado para trabalhar a área ou a circunferência de qualquer círculo. Para encontrar a circunferência de um círculo, use a fórmula C (circunferência) = π vezes o diâmetro. Para encontrar a área de uma circunferência, use a fórmula π (raio²). Esta fórmula é às vezes escrita como A = π r 2 {\displaystyle A=\pi r^{2}}}. onde r é a variável para o raio de qualquer círculo e A é a variável para a área desse círculo.

Para calcular a circunferência de um círculo com um erro de 1 mm:

• são necessários 4 dígitos para um raio de 30 metros
• 10 dígitos para um raio igual ao da terra
• 15 dígitos para um raio igual à distância entre a terra e o sol.

As pessoas geralmente comemoram o 14 de março como Dia Pi porque o 14 de março também está escrito como 3/14, o que representa os três primeiros números 3,14 na aproximação de pi. O Dia Pi começou em 2001.

Páginas relacionadas

• Círculo