Função exponencial

Em matemática, uma função exponencial é uma função que cresce rapidamente. Mais precisamente, é a função exp ( x ) = e x ^{\i1}exp(x)=e^{x}}. $\exp(x)=e^{x}$ e é a constante de Euler, um número irracional que é aproximadamente 2,71828.

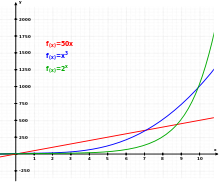
Três funções diferentes: Linear (vermelho), Cúbica (azul) e Exponencial (verde).

Imóveis

Como as funções exponenciais utilizam a exponenciação, elas seguem as mesmas regras. Assim, a exponenciação,

exp ( x + y ) = exp ( x ) exp ( y ) = e x + y {\i1}exp(x+y)=exp(x)xp(x)xp(y)=e^{x+y}}} $\exp(x+y)=\exp(x)\exp(y)=e^{x+y}$ . Isto segue a regra que x a ⋅ x b = x a + b ^{a}{a}{cdot x^{b}=x^{a+b}}} $x^{a}\cdot x^{b}=x^{a+b}$ .

O logaritmo natural é a operação inversa de uma função exponencial.

ln ( x ) = log e ( x ) = log ( x ) log ( e ) {\i1}{e}(x)={\i}log _{e}(x)={\i}frac {\i}{\i(x)}{\i(e)}} $\ln(x)=\log _{e}(x)={\frac {\log(x)}{\log(e)}}$

A função exponencial satisfaz uma propriedade interessante e importante no cálculo diferencial,

d d x e x = e x {\i1}displaystyle {\i}frac {\i}mathrm x}e^{x}=e^{x}}}e^{x}} ${\frac {\mathrm {d} }{\mathrm {d} x}}e^{x}=e^{x}$ ,

Isto significa que a inclinação da função exponencial é a própria função exponencial e, posteriormente, isto significa que tem uma inclinação de 1 a x = 0 {\displaystyle x=0} $x=0$ . Estas propriedades são a razão pela qual ela é uma função importante na matemática.

Aplicações

A função exponencial está entre as mais úteis das funções matemáticas. Ela é usada para representar o crescimento exponencial, que tem usos em praticamente todos os assuntos científicos e também é proeminente em Finanças. A decadência exponencial também acontece, por exemplo, a decadência radioativa e a absorção da luz.

Um exemplo de uma função exponencial na vida real seria o interesse em um banco. Se uma pessoa deposita £100 em uma conta que recebe 3% de juros por mês, então o saldo de cada mês seria (assumindo que o dinheiro não seja tocado):

Mês	Balanço	Mês	Balanço
Janeiro	£100.00	Julho	£119.41
Fevereiro	£103.00	Agosto	£122.99
Março	£106.09	Setembro	£126.68
Abril	£109.27	Outubro	£130.48
Maio	£112.55	Novembro	£134.39
Junho	£115.93	Dezembro	£138.42

Observe como o dinheiro extra dos juros aumenta a cada mês. Quanto maior o saldo original, mais juros a pessoa receberá.

Dois exemplos matemáticos de funções exponenciais são mostrados abaixo.

a=2

x estilo de jogo x	Resultado
-2	0.25
-1	0.5
0	1
1	2
2	4
3	8
4	16

a=3

x estilo de jogo x	Resultado
-2	^1/9
-1	^1/3
0	1
1	3
2	9
3	27
4	81

Relação com a constante matemática e

Embora a base ( um {\displaystyle a} ) possa ser qualquer número maior que zero, por exemplo, 10 ou 1/2, muitas vezes é um número especial chamado e. O número e não pode ser escrito exatamente, mas é quase igual a 2,71828.

O número e é importante para todas as funções exponenciais. Por exemplo, um banco paga juros de 0,01 por cento todos os dias. Uma pessoa pega seu dinheiro de juros e o coloca em uma caixa. Após 10.000 dias (cerca de 30 anos), ele tem 2 vezes mais dinheiro do que começou. Outra pessoa pega o dinheiro de seus juros e o coloca de volta no banco. Como o banco agora lhe paga juros sobre seus juros, a quantidade de dinheiro é uma função exponencial. Após 10.000 dias, ele não tem 2 vezes mais dinheiro do que começou, mas ele tem 2,718145 vezes mais dinheiro do que começou. Este número está muito próximo do número e. Se o banco paga juros mais vezes, então a quantia paga cada vez é menor, então o número estará mais próximo do número e.

Uma pessoa também pode olhar para a foto para ver porque o número e é importante para funções exponenciais. A figura tem três curvas diferentes. A curva com os pontos pretos é uma função exponencial com uma base um pouco menor que e. A curva com as linhas pretas curtas é uma função exponencial com uma base um pouco maior que e. A curva azul é uma função exponencial com uma base exatamente igual a e. A linha vermelha é uma tangente à curva azul. Ela toca a curva azul em um ponto sem cruzá-la. Uma pessoa pode ver que a curva vermelha cruza o eixo x, a linha que vai da esquerda para a direita, em -1. Isto é verdade somente para a curva azul. Esta é a razão pela qual a função exponencial com a base e é especial.

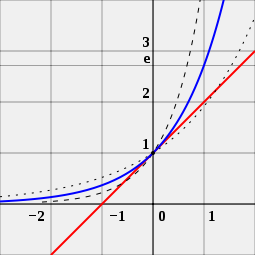
e é o número único a, de modo que o valor da derivada da função exponencial f (x) = eixo (curva azul) no ponto x = 0 é exatamente 1. Para comparação, as funções 2x (curva pontilhada) e 4x (curva tracejada) são mostradas; elas não são tangentes à linha de inclinação 1 (vermelho).

Perguntas e Respostas

P: Qual é a função exponencial?

R: A função exponencial é uma função matemática que cresce cada vez mais rápido.

P: Como é expressa matematicamente a função exponencial?

R: A função exponencial é expressa matematicamente como exp(x) = e^x, onde e é a constante de Euler.

P: O que representa a constante de Euler?

R: A constante de Euler representa um número irracional que é aproximadamente 2,71828.

P: A função exponencial está sempre aumentando?

R: Sim, a função exponencial sempre aumenta de valor na medida em que x aumenta.

P: Há algum limite para a rapidez com que a função exponencial pode crescer?

R: Não, não há limite para a rapidez com que a função exponencial pode crescer, já que ela continua a aumentar com valores maiores de x.

P: Como podemos calcular a constante de Euler?

R: Podemos calcular a constante de Euler usando métodos numéricos, como a série Taylor ou frações contínuas.

P: Que outras aplicações existem para a função exponencial além da matemática?

R: As funções exponenciais têm muitas aplicações fora da matemática, inclusive física, química, biologia, economia e engenharia.