Razão de ouro
Com um número a e outro número b mais pequeno, a proporção dos dois números é encontrada dividindo-os. A sua relação é a/b. Outro rácio é encontrado adicionando os dois números juntos a+b e dividindo este pelo número maior a. O novo rácio é (a+b)/a. Se estes dois rácios forem iguais ao mesmo número, então esse número é chamado o rácio dourado. A letra grega φ {\displaystyle \varphi {\displaystyle \displaystyle \displaystyle \displaystyle} 
(phi) é normalmente usado como o nome da proporção dourada.
Por exemplo, se b = 1 e a/b = φ {\i1}displaystyle {\i}varphi a = φ {\i1}displaystyle {\i}varphi . A segunda razão (a+b)/a é então ( φ + 1 ) / φ {\displaystyle (\varphi +1)/\varphi } 
. Como estes dois rácios são iguais, isto é verdade:
Uma forma de escrever este número é
φ = 1 + 5 2 {\i1}{2}}displaystyle {\i}varphi ={\i1+{\i}frac {\i}{2}}{2
5 
é como qualquer número que, quando multiplicado por si mesmo, faz 5 (ou que número é multiplicado): 5 × 5 = 5 vezes 
A proporção dourada é um número irracional. Se uma pessoa tentar escrevê-la, nunca irá parar e nunca fará um padrão, mas começará desta forma: 1,6180339887... Uma coisa importante sobre este número é que uma pessoa pode subtrair 1 a ele ou dividir 1 por ele. Seja como for, o número continuará e nunca irá parar.
Rectângulo dourado
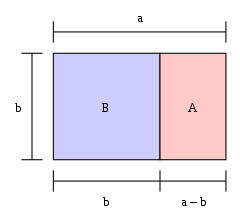
Se o comprimento de um rectângulo dividido pela sua largura for igual à razão áurea, então o rectângulo é um "rectângulo dourado". Se um quadrado for cortado de uma extremidade de um rectângulo dourado, então a outra extremidade é um novo rectângulo dourado. Na imagem, o grande rectângulo (azul e rosa juntos) é um rectângulo dourado porque a / b = φ {\displaystyle a/b=\varphi } 
. A parte azul (B) é um quadrado. A parte rosa por si só (A) é outro rectângulo dourado porque b / ( a - b ) = φ {\displaystyle b/(a-b)=\varphi } 
. O grande rectângulo e o rectângulo rosa têm a mesma forma, mas o rectângulo rosa é mais pequeno e é rodado.
O grande rectângulo BA é um rectângulo dourado; ou seja, a proporção b:a é 1: φ {\i1}displaystyle {\i}varphi . Para qualquer rectângulo, e apenas para rectângulos dessa proporção específica, se removermos o quadrado B, o que resta, A, é outro rectângulo dourado; ou seja, com as mesmas proporções que o rectângulo original.
Números de Fibonacci
Os números Fibonacci são uma lista de números. Uma pessoa pode encontrar o próximo número na lista, adicionando os dois últimos números juntos. Se uma pessoa divide um número da lista pelo número que lhe foi atribuído antes, esta proporção aproxima-se cada vez mais da proporção dourada.
| Número de Fibonacci | dividido pelo anterior | relação |
| 1 | ||
| 1 | 1/1 | = 1.0000 |
| 2 | 2/1 | = 2.0000 |
| 3 | 3/2 | = 1.5000 |
| 5 | 5/3 | = 1.6667 |
| 8 | 8/5 | = 1.6000 |
| 13 | 13/8 | = 1.6250 |
| 21 | 21/13 | = 1.6154... |
| 34 | 34/21 | = 1.6190... |
| 55 | 55/34 | = 1.6177... |
| 89 | 89/55 | = 1.6182... |
| ... | ... | ... |
| φ {\i1}displaystyle {\i1}varphi | = 1.6180... |
Razão de ouro na natureza
Na natureza, a proporção dourada é frequentemente utilizada para o arranjo de folhas ou flores. Estas utilizam o ângulo dourado de aproximadamente 137,5 graus. As folhas ou flores dispostas nesse ângulo utilizam melhor a luz solar.
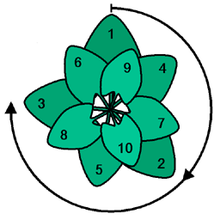
A utilização do ângulo dourado utilizará de forma óptima a luz do sol. Esta é uma vista de cima.
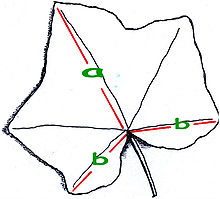
Uma folha de hera comum, mostrando a proporção de ouro
Perguntas e Respostas
P: Qual é a proporção de dois números?
R: A relação de dois números é encontrada dividindo-os, de maneira que a relação seria a/b.
P: Como se pode encontrar outra relação?
R: Outra razão pode ser encontrada somando os dois números e depois dividindo esta soma pelo número maior, a. Esta nova razão seria (a+b)/a.
P: Para que serve o nome quando essas duas relações são iguais uma à outra?
R: Quando essas duas relações são iguais uma à outra, chama-se a relação de ouro. Geralmente é representada com a carta grega צ ou phi.
P: Se b = 1 e a/b = צ , o que isso significa para a?
R: Se b = 1 e a/b = צ , então isso significa que a = צ também.
P: Como se pode escrever esse número de uma maneira?
R: Uma maneira de escrever este número é צ = 1 + 5 / 2 = 1.618...
P: O que significa se o senhor subtrair 1 dele ou dividir 1 por ele?
R: Se o senhor subtrair 1 dele ou dividir 1 por ele, o senhor receberá de volta o mesmo número - em outras palavras, ambos serão iguais à razão de ouro.
P: A ração de ouro é um número irracional?
R: Sim, a ração de ouro é um número irracional, o que significa que se alguém tentar escrevê-lo, nunca haverá um fim e nenhum padrão - apenas começando com algo como "1,6180339887...".
