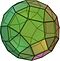
Sólido arquimédico

Em geometria, um sólido arquimédico é uma forma convexa que é composta de polígonos. É um poliedro, com as seguintes propriedades:

Cada rosto é feito de um polígono regular
Todos os cantos da forma parecem os mesmos
A forma não é nem um sólido platônico, nem um prisma, nem um antiprisma.

Dependendo da forma como são contados, existem treze ou quinze formas. De duas dessas formas, existem duas versões, que não podem ser feitas de forma congruente usando rotação. Os sólidos arquimedes recebem o nome do matemático grego antigo Arquimedes, que provavelmente os descobriu no século III a.C. Os escritos de Arquimedes foram perdidos, mas Pappo de Alexandria os resumiu no século IV. Durante a Renascença, artistas e matemáticos valorizavam as formas puras e redescobriram todas essas formas. Johannes Kepler provavelmente completou esta busca por volta de 1620.

A construção de um sólido arquimédico requer pelo menos dois polígonos diferentes.

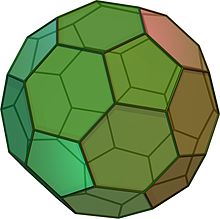
Um icosaedro truncado parece uma bola de futebol. É feita de 12 pentágonos equiláteros e 20 hexágonos regulares. Tem 60 vértices e 90 bordas. É um sólido arquimédico

Imóveis

Os sólidos arquimedesianos são feitos de polígonos regulares, portanto todas as bordas têm o mesmo comprimento.
Todos os sólidos arquimedesianos podem ser produzidos a partir de sólidos platônicos, "cortando as bordas" do sólido platônico.
O tipo de polígonos encontrados em um canto ("vértice") caracteriza tanto o sólido arquimédico quanto o platônico

Relação com sólidos platônicos

Os sólidos platônicos podem ser transformados em sólidos arquimedesianos seguindo uma série de regras para sua construção.

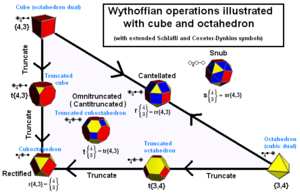
Os sólidos arquimedesianos podem ser construídos como posições geradoras em um caleidoscópio

Lista de sólidos arquimedesanos

A seguir, uma lista de todos os sólidos arquimedeses

Imagem	Nome	Faces	Tipo	Bordas	Vértices
	Tetraedro truncado	8	4 triângulos 4 hexágonos	18	12
	Cuboctahedron	14	8 triângulos 6 quadrados	24	12
	Cubo truncado	14	8 triângulos 6 octógonos	36	24
	Octádron truncado	14	6 quadrados 8 hexágonos	36	24
	Rhombicuboctahedron	26	8 triângulos 18 quadrados	48	24
	Cuboctaedro truncado	26	12 quadrados 8 hexágonos 6 octógonos	72	48
	Snub cube (2 versões espelhadas)	38	32 triângulos 6 quadrados	60	24
	Icosidodecaedro	32	20 triângulos 12 pentagões	60	30
	Dodecaedro truncado	32	20 triângulos 12 decágonos	90	60
	icosaedro truncado	32	12 pentagões 20 hexágonos	90	60
	Rhombicosidodecaedro	62	20 triângulos30 quadrados12 pentagons	120	60
	icosidodecaedro truncado	62	30 quadrados 20 hexágonos 12 decágonos	180	120
	Snub dodecahedron (2 versões espelhadas)	92	80 triângulos 12 pentagões	150	60

Perguntas e Respostas

P: O que é um arquimédico sólido?

R: Um sólido arquimédico é uma forma convexa feita de polígonos que tem as propriedades de cada face sendo um polígono regular, todos os cantos parecendo o mesmo, e não sendo um sólido platônico, prisma ou antiprisma.

P: Quantos sólidos arquimedesianos existem?

R: Dependendo de como eles são contados, há treze ou quinze sólidos arquimedesanos.

P: Quem descobriu os sólidos arquimedeses?

R: Os sólidos arquimedes têm o nome do matemático grego antigo Arquimedes, que provavelmente os descobriu no século III a.C.

P: O que Pappus de Alexandria fez com os escritos de Arquimedes?

R: Pappus de Alexandria resumiu os escritos de Arquimedes sobre os sólidos de Arquimedes no século IV a.C..

P: Por que artistas e matemáticos redescobriram os sólidos de Arquimedes durante a Renascença?

R: Durante a Renascença, artistas e matemáticos valorizavam as formas puras, e os sólidos arquimedesianos eram considerados formas puras.

P: Quando Johannes Kepler completou a busca de todos os sólidos arquimedesanos?

R: Johannes Kepler provavelmente completou a busca de todos os sólidos arquimedeses por volta de 1620.

P: O que é necessário para construir um sólido arquimediano?

R: A construção de um sólido arquimédico requer pelo menos dois polígonos diferentes.