Relógio de luz

O relógio de luz é uma forma simples de mostrar uma característica básica da relatividade Especial. Um relógio é concebido para funcionar ao fazer saltar um clarão de luz de um espelho distante e usando o seu retorno para desencadear outro clarão de luz, contando entretanto quantos clarões ocorreram ao longo do caminho. É fácil mostrar que as pessoas na Terra a verem uma nave espacial voar por cima com um relógio deste tipo vê-lo-iam a fazer tic-tac relativamente devagar. A este efeito chama-se dilatação dotempo.

Antes de estudarmos o relógio de luz, consideremos outro tipo de relatividade. Imagine que alguém está a driblar uma bola de basquetebol no porão de um grande jacto de carga. O jogador de basquetebol está a mover-se na mesma direcção que o avião a jacto. As outras pessoas no avião vêem-no a mover-se um metro ou dois enquanto ele faz um driblar. Entre o momento em que a bola salta da primeira vez e o momento em que a bola salta da segunda vez, já passou cerca de um segundo. Mas quando ocorreu o primeiro ressalto, a bola de basquetebol estava sobre Gibraltar, e quando ocorreu o segundo ressalto, a bola de basquetebol estava sobre a água mais próxima de Espanha. Assim, a bola de basquetebol deslocou-se 280 metros em relação à Terra.

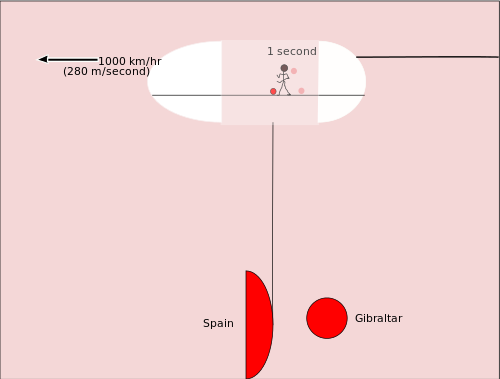
Agora considere uma questão um pouco semelhante de movimento relativo. Desta vez vamos considerar o que as pessoas que olham para as estrelas do Pólo Norte vêem quando uma nave espacial muito rápida sobre elas voa. Podemos usar álgebra e o teorema de Pitágoras para calcular quanto tempo demora na nave espacial. A única outra coisa de que precisamos é da equação que relaciona distância, d, taxa ou velocidade de viagem, r, e tempo, t. A equação é:

d = rt

A velocidade da luz é constante, por isso vamos aplicar este valor a dois problemas. Chamaremos velocidade da luz c, uma vez que esta é a letra que os cientistas normalmente usam para a nomear.

Um relógio é feito colocando uma saída de luz no fundo de um longo poste, um espelho no topo do poste, e um detector de luz electrónico no fundo do poste. O relógio é iniciado fechando brevemente um interruptor que envia um piscar de luz da base do poste para o topo do poste, onde é reflectido de volta para a base do poste. Quando o detector de luz na parte inferior do poste vê o piscar de luz, faz duas coisas. Adiciona uma ao contador que lhe está ligado, e dispara outro piscar de luz até ao espelho. Quando esse piscar de luz volta ao fundo, a contagem muda para dois, e outro piscar de luz é desencadeado. Uma vez que a luz viaja muito rapidamente (300.000 quilómetros/segundo), por cada segundo medido por um relógio normal, o relógio de luz "assinala" um número muito grande de vezes.

Para facilitar a matemática, diremos que o pólo tem um quilómetro e meio de comprimento. Assim, se estivermos junto ao relógio de luz que é construído junto ao grande telescópio no Pólo Norte, veremos que a luz percorre um quilómetro por cada "tique" do relógio de luz. Uma vez que a distância percorrida, d, é igual à velocidade multiplicada pelo tempo, e a velocidade envolvida é c, temos a equação:

d = ct

e podemos resolver esta equação durante t para aprender quanto tempo em segundos cada "tick" é longo.

1 km = 300.000 km/segundo * t segundos

t segundos = 1 km/300,000 (km/segundo) = 1/300,000 segundos = 0,00000333...3 segundos

Por outras palavras, cada "tique" do relógio luminoso levará 0,00000333...3 segundos.

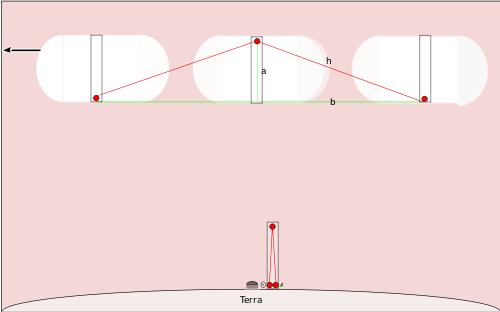
Se uma nave espacial voasse numa linha recta passando sobre o Pólo Norte a uma grande fracção da velocidade da luz, e tivesse um relógio semelhante, as pessoas que observavam a sua passagem veriam que o espelho no topo do pólo se tinha deslocado directamente sobre a luz emissora, pelo que a luz viajaria ao longo da linha marcada h no diagrama, e depois seguiria a outra hipotenusa até à base do pólo - que já se teria deslocado alguma distância uma vez que a nave espacial se está a deslocar tão rapidamente. Podemos descobrir quanto tempo levaria um tique de acordo com as pessoas na Terra. Sabemos que o pólo da nave espacial tem um comprimento de um, uma vez que é o mesmo tipo de relógio que as pessoas estão a usar no Pólo Norte. Queremos descobrir t' , o tempo que leva a fazer um tique do relógio na nave espacial.

Sabemos que a nave espacial viajará 1/2 r t' enquanto o piscar da luz se dirige para cima em direcção ao espelho, e outra 1/2 r t' enquanto o piscar da luz se dirige para baixo em direcção à base do pólo. Assim, esse cálculo dá-nos o comprimento da linha b no gráfico. Conhecemos a, para que possamos perceber h pelo teorema de Pitágoras:

h = √(a2 + (rt' /2)²)

Assim, a distância total percorrida pela luz é de 2 h ou d = 2 √(a2 + (rt' /2)²)

Sabemos também que a velocidade da luz, c, é constante. Não importa quem a mede, revela-se ser a mesma velocidade. Portanto, podemos usar esse facto para obter outra forma de calcular quanto tempo demora o clarão da luz a passar da base para o topo do poste e para trás novamente:

t' = d/c

Por outras palavras, d = c t' .

Para que possamos escrever

c t' = 2 √(a2 + (rt' /2)²)

1/2 c t' = √(a2 + (rt' /2)²)

Para resolver a equação acima, teremos de o fazer:

Quadrado de ambos os lados
Dividir ambos os lados por t' ²
Multiplicar ambos os lados por 4
Dividir ambos os lados por c2
Simplificar c2 / c2
Subtrair r2/c2 de ambos os lados
Tomar a raiz quadrada de ambos os lados
Multiplicar ambos os lados por t'
Divida ambos os lados por √(1-r2/c2)

Resolvendo a equação acima, descobrimos que:

t' = 2a/(c√(1-r2/c2)

O tempo entre os tiques do relógio no Pólo Norte é de 2a/c, pelo que podemos então escrever:

t' = t/√(1-r2/c2)

Se t = 1 segundo, então se a nave espacial estiver a viajar a metade da velocidade da luz, t' = 1,1547 seg.

Experiência com várias velocidades de viagem em: http://www.1728.org/reltivty.htm

Perguntas e Respostas

P: O que é uma campainha de luz?

R: Um relógio leve é um dispositivo destinado a demonstrar uma propriedade fundamental de relatividade especial. Ela funciona refletindo um clarão de luz de um espelho distante e usando seu retorno para desencadear outro clarão de luz, enquanto conta quantos clarões ocorreram ao longo do caminho.

P: O que é dilatação do tempo?

R: A dilatação do tempo é um fenômeno que ocorre quando as pessoas na Terra observam uma nave espacial voar por meio de um relógio de luz. Eles o vêem fazendo tic-tac relativamente devagar sob a influência da relatividade.

P: Como podemos calcular quanto tempo se passa em uma nave espacial?

R: Podemos usar álgebra e o teorema de Pitágoras para calcular quanto tempo fica mais lento em uma nave espacial. Precisamos aplicar a equação d = rt (distância igual a tempo de velocidade) e usar a velocidade constante da luz c em dois problemas.

P: Como funciona um relógio de luz?

R: Um relógio de luz consiste de uma fonte de luz na parte inferior de uma haste longa com um espelho na parte superior e um detector eletrônico na parte inferior. Quando é ligado, um único clarão de luz passa de baixo para cima, onde é refletido de volta para baixo quando é detectado pelo detector em baixo, o que acrescenta um contador ao contador anexo e desencadeia outro clarão de novo para cima. Esse processo continua até que ele seja interrompido ou reiniciado.

P: De que equação precisamos para este cálculo?

R: Precisamos de t' = 2a/(c√(1-r2/c2)), onde t' (o tempo entre ticks do relógio do Pólo Norte) é igual a 2a/c dividido por √(1-r2/c2). Se t = 1 segundo, e viajando à metade da velocidade da luz, t' = 1,1547 segundos.

P. Como se relaciona o teorema de Pitágoras com este cálculo?

R: O teorema de Pitágoras nos ajuda a encontrar h (a hipotenusa), que faz parte da equação que nos permite calcular quanto tempo dura cada carrapato em segundos (d=ct). Uma vez que sabemos h, podemos resolver por t', o que nos diz quanto tempo dura cada ponto de acordo com as pessoas da Terra que olham do Pólo Norte e as pessoas do próprio navio, que está passando por cima delas muito rapidamente.