Momento magnético
O momento magnético de um ímã é uma quantidade que determina a força que o ímã pode exercer sobre as correntes elétricas e o torque que um campo magnético irá exercer sobre ele. Um laço de corrente elétrica, um ímã de barra, um elétron, uma molécula e um planeta, todos têm momentos magnéticos.
Tanto o momento magnético quanto o campo magnético podem ser considerados como vetores com uma magnitude e direção. A direção do momento magnético aponta do pólo sul para o pólo norte de um imã. O campo magnético produzido por um ímã é proporcional a seu momento magnético também. Mais precisamente, o termo momento magnético normalmente se refere ao momento dipolo magnético de um sistema, que produz o primeiro termo na expansão multipolar de um campo magnético geral. O componente dipolo do campo magnético de um objeto é simétrico em relação à direção de seu momento dipolo magnético, e diminui conforme o cubo inverso da distância do objeto.
Duas definições de momento
Nos livros de texto, duas abordagens complementares são utilizadas para definir os momentos magnéticos. Nos livros de texto anteriores a 1930, elas eram definidas usando pólos magnéticos. Os livros didáticos mais recentes o definem em termos de correntes Ampèrianas.
Definição do pólo magnético
Os físicos representam fontes de momentos magnéticos em materiais como postes. Os pólos Norte e Sul são uma analogia com as cargas positivas e negativas na eletrostática. Considere um imã de barra que possui pólos magnéticos de igual magnitude, mas de polaridade oposta. Cada pólo é a fonte de força magnética que se enfraquece com a distância. Como os pólos magnéticos sempre vêm em pares, suas forças se anulam parcialmente porque enquanto um pólo puxa, o outro se repele. Este cancelamento é maior quando os pólos estão próximos um do outro, ou seja, quando o ímã de barra é curto. A força magnética produzida por um ímã de barra, em um determinado ponto no espaço, depende, portanto, de dois fatores: tanto da força p

m = p l . mmathbf {m} =pmathbf {l} . }
Aponta na direção do pólo Sul para o pólo Norte. A analogia com os dipolos elétricos não deve ser levada muito longe porque os dipolos magnéticos estão associados ao momento angular (ver Momento magnético e momento angular). No entanto, os pólos magnéticos são muito úteis para cálculos magnetostáticos, particularmente em aplicações com ferromagnetos. Os praticantes que utilizam a abordagem do pólo magnético geralmente representam o campo magnético pelo campo irrotacional H {\i1}mathbf {\i} } 

Definição do loop atual
Suponha que um circuito fechado planar carregue uma corrente elétrica I no estilo I 








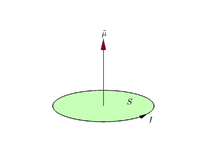
m = I S . mmathbf {m} =Imathbf {S} . }
Por convenção, a direção da área vetorial é dada pela regra da mão direita (enrolar os dedos da mão direita na direção da corrente ao redor do laço, quando a palma da mão está "tocando" a borda externa do laço, e o polegar reto indica a direção da área vetorial e, portanto, do momento magnético).
Se o laço não for plano, o momento é dado como
m = I 2 ∫ r × d r . mathbf {m} =frac {I}{2}int {mathbf {r} \vezes, o tempo de trabalho. }
No caso mais geral de uma distribuição de corrente arbitrária no espaço, o momento magnético de tal distribuição pode ser encontrado a partir da seguinte equação:
m = 1 2 ∫ r × J d V , {\i1} ={\i1}frac {\i}{\i1}displaystyle {\i}mathbf {\i} ={\i1}frac {\i}int {\i}mathbf \vezes matemathbf \V,V,V,V,V,V,V,V,V,V
onde r {\i1}displaystyle {r}mathbf 

A equação acima pode ser usada para calcular um momento magnético de qualquer conjunto de cargas móveis, como um sólido com carga de fiação, substituindo
J = ρ v , {\i1}displaystyle {\i}mathbf {\i} =rho {\i}mathbf {v} ,}
onde ρ 

Por exemplo, o momento magnético produzido por uma carga elétrica movendo-se ao longo de um caminho circular é
m = 1 2 q r × v {\i1}{\i1} = 1 2 q r × v {\i}displaystyle {\i}mathbf {\i} = 1 2 q r × v {\i}mathbf \vezes matemathbf 
onde r {\i1}displaystyle {r}mathbf 


Os praticantes que utilizam o modelo atual de laço geralmente representam o campo magnético pelo campo solenoidal B {\i1}mathbf {\i} } 

Momento magnético de um solenóide
Uma generalização do laço atual acima é uma bobina multi-voltas, ou solenóide. Seu momento é a soma vetorial dos momentos de curvas individuais. Se o solenóide tem N {\displaystyle N} 
m = N I S . mathbf {m} =NImathbf {S} . }
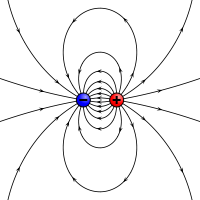
Um análogo eletrostático para um momento magnético: duas cargas opostas separadas por uma distância finita.
.svg.png)
Imagem 3-D de um solenóide.
Unidades
A unidade para o momento magnético não é uma unidade base no Sistema Internacional de Unidades (SI) e pode ser representada de mais de uma forma. Na equação do torque em um momento, o torque é medido em Newton.meters e o campo magnético em tesla, assim o momento é medido em N.m por Tesla ( N.m T - 1 {\i1}{\i1}displaystyle {\i1}{\i1}}}^{\i1}
A m 2 = N.m T - 1 . estilo de jogo, texto ^{2}=,texto ^{N.m T}^{-1}. }
No sistema CGS, existem vários conjuntos diferentes de unidades de eletromagnetismo, dos quais os principais são ESU, Gaussian, e EMU. Entre elas, há duas unidades alternativas (não equivalentes) de momento dipolo magnético no CGS:
(ESU CGS) 1 statA-cm² = 3,33564095×10-14 (m2-A ou N.m/T)
e (mais freqüentemente utilizado)
(EMU CGS e Gaussian-CGS) 1 erg/G = 1 abA-cm² = 10-3 (m2-A ou N.m/T).
A relação dessas duas unidades CGS não equivalentes (UME/ESU) é igual exatamente à velocidade da luz em espaço livre, expressa em cm/s.
Todas as fórmulas deste artigo estão corretas em unidades SI, mas em outros sistemas de unidades, as fórmulas podem precisar ser alteradas. Por exemplo, em unidades SI, um loop de corrente com corrente I e área A tem momento magnético I×A (veja abaixo), mas em unidades Gaussianas o momento magnético é I×A/c.
| Momentos magnéticos intrínsecos e giros de algumas partículas elementares | ||
| Partícula | Momento dipolo magnético em unidades SI (10-27 J/T) | Número quantum giratório (sem dimensão) |
| -9284.764 | 1/2 | |
| protão | 14.106067 | 1/2 |
| nêutron | -9.66236 | 1/2 |
| muon | -44.904478 | 1/2 |
| deuteron | 4.3307346 | 1 |
| triton | 15.046094 | 1/2 |
Para a relação entre as noções de momento magnético e magnetização, ver magnetização.
Perguntas e Respostas
P: O que é o momento magnético de um ímã?
R: O momento magnético de um ímã é uma quantidade que determina a força que o ímã pode exercer sobre as correntes elétricas e o torque que um campo magnético exercerá sobre ele.
P: Quais objetos têm momentos magnéticos?
R: Um loop de corrente elétrica, um ímã em barra, um elétron, uma molécula e um planeta, todos têm momentos magnéticos.
P: Como o momento magnético e o campo magnético podem ser considerados?
R: Tanto o momento magnético quanto o campo magnético podem ser considerados vetores com magnitude e direção.
P: Em que direção aponta o momento magnético em um ímã?
R: A direção do momento magnético aponta do polo sul para o polo norte de um ímã.
P: Qual é a relação entre o momento magnético e o campo magnético de um ímã?
R: O campo magnético produzido por um ímã é proporcional ao seu momento magnético.
P: A que o termo momento magnético normalmente se refere?
R: Mais precisamente, o termo momento magnético normalmente se refere ao momento de dipolo magnético de um sistema, que produz o primeiro termo na expansão multipolar de um campo magnético geral.
P: Como o componente dipolo do campo magnético de um objeto se comporta à medida que a distância do objeto aumenta?
R: O componente de dipolo do campo magnético de um objeto é simétrico em relação à direção de seu momento de dipolo magnético e diminui como o cubo inverso da distância do objeto.
Pesquise na enciclopédia