Produto ponto

Em matemática, o produto ponto é uma operação que leva dois vetores como entrada, e que retorna um número escalar como saída. O número retornado depende do comprimento dos dois vetores, e do ângulo entre eles. O nome é derivado do ponto centralizado "-" que é freqüentemente usado para designar esta operação; o nome alternativo produto escalar enfatiza a natureza escalar (ao invés de vetor) do resultado.

O produto ponto contrasta (no espaço tridimensional) com o produto cruzado, que produz um vetor como resultado.

Definição

O ponto produto de dois vetores a = [a1, a2, ..., a] e b = [b1, b2, ..., bn] é definido como:

a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n {\i1}mathbf {a} {\i}cdot {\i}mathbf {b} =sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\i}cdots +a_{n}b_{n}}}} {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}}

onde Σ denota a notação de soma (a soma de todos os termos) e n é a dimensão do espaço vetorial.

Na dimensão 2, o ponto produto dos vetores [a,b] e [c,d] é ac + bd. Da mesma forma, em uma dimensão 3, o produto ponto de vetores [a,b,c] e [d,e,f] é ad + be + cf. Por exemplo, o produto ponto de dois vetores tridimensionais [1, 3, -5] e [4, -2, -1] é

[ 1 , 3 , − 5 ] ⋅ [ 4 , − 2 , − 1 ] = ( 1 × 4 ) + ( 3 × ( − 2 ) ) + ( ( - 5 ) × ( - 1 ) ) = ( 4 ) - ( 6 ) + ( 5 ) = 3. {\i1,3,-5]{\i1}cdot [4,-2,-1]=(1\i1 vezes 4)+(3\i1)+((-5)\i1)=(4)-(6)+(5)=3.} {\displaystyle [1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.}

Interpretação geométrica

Na geometria euclidiana, o produto do ponto, o comprimento e o ângulo estão relacionados. Para um vetor a, o produto do ponto a - a é o quadrado do comprimento de um, ou

a ⋅ a = ‖ a ‖ 2 {\i1}displaystyle {\i1}mathbf {a}cdot {\i}mathbf {a Esquerda {\displaystyle {\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}}

onde |||a|| denota o comprimento (magnitude) de a. Mais geralmente, se b é outro vetor

a ⋅ b = ‖ a ‖ a ‖ b ‖ b ‖ cos θ {\i1}displaystylemathbf {a}cdot {\i1}mathbf {b} =esquerda \Certo, vamos lá...} {\displaystyle \mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|\cos \theta \,}

onde |||a|||| e |b||| denota o comprimento de a e b e θ é o ângulo entre eles.

Esta fórmula pode ser rearranjada para determinar o tamanho do ângulo entre dois vetores não zeros:

θ = arccos ( a ⋅ b ‖ a ‖ ‖ a ‖ b ‖ ) {\i1}displaystyle {\i1}displaystyle {\i1}displaystyle {\i1}theta = arccos esquerda(a) {\displaystyle \theta =\arccos \left({\frac {{\mathbf {a}}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}\right\|\left\|{\mathbf {b}}\right\|}}\right)}

Também se pode primeiro converter os vetores em vetores de unidade dividindo por sua magnitude:

a ^ = a ‖ a ‖ a ‖ símbolo de fração {\displaystyle {\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\|}}}

então o ângulo θ é dado por

θ = arccos ( a ^ ⋅ b ^ ) {\i1}displaystyle {\i1}theta =arccos(símbolo das fechaduras {\i1}cdot {\i}cdot {\i}boldsymbol {\i} {\displaystyle \theta =\arccos({\boldsymbol {\hat {a}}}\cdot {\boldsymbol {\hat {b}}})}

Como o cosseno de 90° é zero, o produto de dois vetores ortogonais (perpendiculares) é sempre zero. Além disso, dois vetores podem ser considerados ortogonais se e somente se seu produto de ponto for zero, e ambos tiverem um comprimento não zero. Esta propriedade fornece um método simples para testar a condição de ortogonalidade.

Algumas vezes estas propriedades também são usadas para definir o produto ponto, especialmente em 2 e 3 dimensões; esta definição é equivalente à anterior. Para dimensões superiores, a fórmula pode ser usada para definir o conceito de ângulo.

As propriedades geométricas dependem da base ser orto-normal, ou seja, composta de vetores perpendiculares em pares com comprimento unitário.

Projeção escalar

Se tanto a como b têm comprimento um (ou seja, são vetores de unidade), seu produto ponto simplesmente dá o cosseno do ângulo entre eles.

Se apenas b é um vetor unitário, então o produto ponto a - b dá |a| cos(θ), ou seja, a magnitude da projeção de a na direção de b, com um sinal de menos se a direção for oposta. Isto é chamado de projeção escalar de a em b, ou componente escalar de a na direção de b (ver figura). Esta propriedade do produto ponto tem várias aplicações úteis (por exemplo, veja a próxima seção).

Se nem a nem b é um vetor unitário, então a magnitude da projeção de a na direção de b, por exemplo, seria a - (b / |b|) como o vetor unitário na direção de b é b / |b|.

Rotação

Uma rotação da base orthonormal em termos de qual vetor a é representado é obtida com a multiplicação de a por uma matriz de rotação R. Esta multiplicação de matriz é apenas uma representação compacta de uma seqüência de produtos de ponto.

Por exemplo, deixe

  • B1 = {x, y, z} e B2 = {u, v, w} são duas bases orto-normais diferentes do mesmo espaço R3, com B2 obtida apenas girando B1,
  • a1 = (ax, ay, az) representam o vetor a em termos de B1,
  • a2 = (au, av, aw) representam o mesmo vetor em termos da base girada B2,
  • u1, v1, w1 sejam os vetores de base rotativa u, v, w representados em termos de B1.

Em seguida, a rotação de B1 para B2 é realizada da seguinte forma:

a 2 = R a 1 = [ u x u y u z v x v y v z w x w y w z ] [ a x a y a z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf 1cdot {1}{1}mathbf {a}{1}mathbf {w}_{1}cdot {1}mathbf {a}{1}end{bmatrix}=begin{bmatrix}a_u}a_vmathbf } {\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}\\a_{v}\\a_{w}\end{bmatrix}}.}

Observe que a matriz de rotação R é montada usando os vetores de base rotativa u1, v1, w1 como suas fileiras, e esses vetores são vetores unitários. Por definição, Ra1 consiste de uma seqüência de produtos de pontos entre cada uma das três fileiras de R e o vetor a1. Cada um desses produtos de ponto determina um componente escalar de um na direção de um vetor de base girada (ver seção anterior).

Se a1 é um vetor de linha, e não um vetor de coluna, então R deve conter os vetores de base girada em suas colunas, e deve pós-multiplicar a1:

a 2 = a 1 R = [ a x a y a z ] [ u x v x w x u y v y w y u z v z w z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}mathbf {\i1}}_{\i1}{\i1}}{\i1}{\i1}{\i1}{\i1}}mathbfa_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_z_end{bmatrix}={begin{bmatrix}{mathbf {u}_{1}cdot {mathbf {a}_{1}&mathbf {v}_{1}cdot {mathbf {a}_{1}{1}cdot {mathbf {a}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}. } {\displaystyle {\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}.}

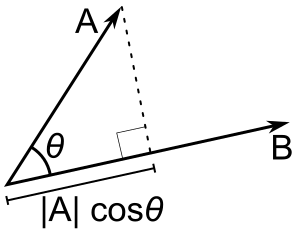
A - B = |A| | B| cos(θ). | A| cos(θ) é a projeção escalar de A sobre B.Zoom
A - B = |A| | B| cos(θ). | A| cos(θ) é a projeção escalar de A sobre B.

Física

Em física, a magnitude é um escalar no sentido físico, ou seja, uma quantidade física independente do sistema de coordenadas, expressa como o produto de um valor numérico e uma unidade física, não apenas um número. O produto ponto é também um escalar neste sentido, dado pela fórmula, independente do sistema de coordenadas. Exemplo:

Imóveis

As seguintes propriedades se mantêm se a, b, e c são vetores reais e r é um escalar.

O produto ponto é comutativo:

a ⋅ b = b ⋅ a . {\i1}displaystyle {\i}mathbf {a}cdot {\i}mathbf {b} =mathbf {b} \cdot {a} . } {\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} .}

O produto ponto é distributivo sobre a adição vetorial:

a ⋅ ( b + c ) = a ⋅ b + a ⋅ c . estilo de jogo {\a} {a} {cdot (mathbf {b} +\mathbf {c} )=mathbf {a}cdot {cdot {b} +\i1mathbf {a}cdot {cdot {c}mathbf {c} . } {\displaystyle \mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} .}

O produto ponto é bilinear:

a ⋅ ( r b + c ) = r ( a ⋅ b ) + ( a ⋅ c ) . {\a} {a} {a} {a} +(r=mathbf {b} +(mathbf {c} )=r(mathbf {a} {a} {cdot {mathbf {b} )+(mathbf {a} {a} {cdot {cdot {mathbf {c} ). } {\displaystyle \mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ).}

Quando multiplicado por um valor escalar, o produto ponto satisfaz:

( c 1 a ) ⋅ ( c 2 b ) = ( c 1 c 2 ) ( a ⋅ b ) {\i1}{\i1}displaystyle (c_{1}mathbf {a} ){cdot (c_{2}mathbf {b} )=(c_{1}c_{2})({\i}mathbf {a} {cdot {b} )}(c_{2}mathbf {b {\displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )}

(estas duas últimas propriedades seguem das duas primeiras).

Dois vetores não-zero a e b são perpendiculares se e somente se a - b = 0.

Ao contrário da multiplicação de números comuns, onde se ab = ac, então b é sempre igual a c a menos que a seja zero, o produto ponto não obedece à lei de cancelamento:

Se a - b = a - c e a ≠ 0, então podemos escrever: a - (b - c) = 0 pela lei distributiva; o resultado acima diz que isto significa apenas que a é perpendicular a (b - c), o que ainda permite (b - c) ≠ 0, e portanto b ≠ c.

Desde que a base seja orthonormal, o produto ponto é invariante sob mudanças isométricas da base: rotações, reflexos e combinações, mantendo a origem fixa. A interpretação geométrica acima mencionada se baseia nesta propriedade. Em outras palavras, para um espaço orthonormal com qualquer número de dimensões, o produto ponto é invariante sob uma transformação de coordenadas baseada em uma matriz ortogonal. Isto corresponde às duas condições a seguir:

  • A nova base é novamente orthonormal (ou seja, é orthonormal expressa na antiga).
  • Os novos vetores base têm o mesmo comprimento que os antigos (ou seja, comprimento da unidade em termos da base antiga).

Se a e b são funções, então a derivada de a - b é a' - b + a - b'

Tríplice expansão de produtos

Esta é uma identidade muito útil (também conhecida como a fórmula de Lagrange) envolvendo os produtos ponto e cruzados. Ela está escrita como

a × ( b × c ) = b ( a ⋅ c ) - c ( a ⋅ b ) {\i1}displaystyle {a}mathbf {a} times (mathbf {b} {b} times {c} =mathbf {b} (a) -mathbf {a} {cdot {c}mathbf {c} -mathbf (a) cdot {a}mathbf {b} )} {\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )}

o que é mais fácil de lembrar como "BAC menos CAB", tendo em mente quais vetores estão pontilhados juntos. Esta fórmula é comumente usada para simplificar os cálculos vetoriais em física.

Comprovação da interpretação geométrica

Considere o elemento do Rn

v = v 1 e ^ 1 + v 2 e ^ 2 + . . + v n e ^ n . estilo de jogo {v} =v_{1}mathbf {e} + v_mathbf {\i1}mathbf {e} ...+...+v_mathbf _{n}.\,} {\displaystyle \mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,}

Aplicação repetida do teorema de Pitágoras para seu comprimento |v|

| v | 2 = v 1 2 + v 2 2 2 + . . + v n 2 . estilo de jogo |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,} {\displaystyle |\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,}

Mas isto é o mesmo que

v ⋅ v = v 1 2 + v 2 2 2 + . . . + v n 2 , {\\i1}displaystyle {\i}mathbf {v} {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},^,} {\displaystyle \mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,}

Assim, concluímos que, tomando o produto pontilhado de um vetor v consigo mesmo, obtém-se o comprimento quadrado do vetor.

Lemma 1

v ⋅ v = | v | v | 2 . |mathbf {v}cdot |mathbf {v} = |mathbf {v} |^{2}.\,} {\displaystyle \mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,}

Agora considere dois vetores a e b que se estendem desde a origem, separados por um ângulo θ. Um terceiro vetor c pode ser definido como

c = d e f a - b . estilo de exibição {\i1}mathbf {\i} \ decifração ....-mathbf {\displaystyle \mathbf {c} \ {\stackrel {\mathrm {def} }{=}}\ \mathbf {a} -\mathbf {b} .\,}

criando um triângulo com lados a, b, e c. De acordo com a lei de cosseno, temos

c | c | 2 = | a | 2 + | b | 2 - 2 | a | | | b | cos θ . estilo de jogo |^{2}===mathbf {a} |^{2}+|mathbf {b} |^{2}-2|mathbf {a} ||mathbf {b} |\Os custos de .theta...} {\displaystyle |\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Substituindo os produtos de ponto pelos comprimentos quadrados de acordo com Lemma 1, obtemos

c ⋅ c = a ⋅ a + b ⋅ b - 2 | a | | | b | cos θ . estilo de exibição |mathbf {c} \cdot {cdot {c}mathbf {c} =mathbf {a} {cdot {a}mathbf {a} +mathbf {b} \cdot {b} -2|mathbf {a} ||mathbf {b} |\{\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}(1)

Mas como c ≡ a - b, também temos

c ⋅ c = ( a - b ) ⋅ ( a - b ) {\i1}displaystyle {\i}mathbf {c} \cdot {cdot {c} =(mathbf {a} -mathbf {b} ){cdot (mathbf {a} -mathbf {b} ){b},} {\displaystyle \mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,},

que, de acordo com a lei distributiva, se expande para

c ⋅ c = a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) . estilo de exibição {\i1}mathbf {c} \cdot {cdot {c}mathbf {c} =mathbf {a} {cdot {a}mathbf {a} +mathbf {b} \({\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,}2)

Fundindo as duas equações c - c, (1) e (2), obtemos

a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) = a ⋅ a + b ⋅ b - 2 | a | | | b | cos θ . estilo de exibição |mathbf |cdot |mathbf | +\a |mathbf |b \2(mathbf {a) {b} -2(mathbf {a) {cdot {b} =mathbf {a) {cdot {cdot {mathbf {a) +mathbf {b} \cdot {b} -2|mathbf {a} ||mathbf {b} |\Os custos de .theta...} {\displaystyle \mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Subtraindo a - a + b - b de ambos os lados e dividindo por -2 folhas

a ⋅ b = | a | | | b | cos θ . mathbf |mathbf {a}cdot |mathbf {b} = |mathbf {a} ||mathbf {b} |\Os custos de .theta...} {\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Q.E.D.

Generalização

O produto interno generaliza o produto ponto a espaços vetoriais abstratos e é normalmente denotado por ⟨ a , b ⟩ \Roteiro} {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle }. Devido à interpretação geométrica do produto ponto a norma ||a|| de um vetor a em tal espaço de produto interno é definida como

‖ a ‖ = ⟨ a , a ⟩ {\displaystyle \|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}}

de tal forma que generaliza o comprimento, e o ângulo θ entre dois vetores a e b por

cos θ = ⟨ a , b ⟩ ‖ a ‖ a ‖ ‖ b ‖ . estilo de jogo,,mathbff,,mathbf \Mathbf, mathbf, mathbf, mathbf, mathbf \|}}. } {\displaystyle \cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b} \rangle }{\|\mathbf {a} \|\,\|\mathbf {b} \|}}.}

Em particular, dois vetores são considerados ortogonais se seu produto interno for zero

⟨ a , b ⟩ = 0. {\a},,{\b}mathbf,,{\b}mathbf =0.} {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle =0.}

Para vetores com entradas complexas, usar a definição dada do produto ponto levaria a propriedades geométricas bastante diferentes. Por exemplo, o produto do ponto de um vetor com si mesmo pode ser um número complexo arbitrário, e pode ser zero sem que o vetor seja o vetor zero; isto, por sua vez, teria conseqüências severas para noções como comprimento e ângulo. Muitas propriedades geométricas podem ser salvas, ao custo de se abrir mão das propriedades simétricas e bilineares do produto escalar, definindo alternativamente

a ⋅ b = ∑ a i b i ¯ {\i}displaystyle {\i}mathbf {a}cdot {\i}mathbf {b} =sum {a_{\i}{\i}{\i_sobreline {b_{\i}}}}} {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}}

onde bi é o complexo conjugado de bi. Então o produto escalar de qualquer vetor com si mesmo é um número real não-negativo, e é não-negativo, exceto pelo vetor zero. Entretanto, este produto escalar não é linear em b (mas sim conjugado linear), e o produto escalar também não é simétrico, uma vez que

a ⋅ b = b ⋅ a ¯ ¯displaystyle ¯mathbf {a} ¯cdot ¯mathbf {b} ={\i1}overline ¯mathbf {b} \cdot {a}mathbf }}} {\displaystyle \mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}}.

Este tipo de produto escalar é, no entanto, bastante útil, e leva às noções de forma hermitiana e de espaços internos gerais do produto.

O produto interno Frobenius generaliza o produto ponto para matrizes. Ele é definido como a soma dos produtos dos componentes correspondentes de duas matrizes com o mesmo tamanho.

Generalização a tensores

O produto ponto entre um tensor de ordem n e um tensor de ordem m é um tensor de ordem n+m-2. O produto ponto é trabalhado multiplicando-se e somando-se através de um único índice em ambos os tensores. Se A {\an8}mathbf {A} {\displaystyle \mathbf {A} }e B estilo de jogo B {\displaystyle \mathbf {B} }são dois tensores com representação de elementos A i j ... k ℓ ... ^displaystyle A_{ij{\i}displaystyle A_{ij{\i}^displaystyle {\displaystyle A_{ij\dots }^{k\ell \dots }}B_mn{\i} ^p{\i}displaystyle B_mn{\i}displaystyle B_{\i} ^p{\i}displaystyle{\displaystyle B_{mn\dots }^{p{\dots }i}}A ⋅ B {\i1}displaystyle B_mathbf {\i} \cdot {B}mathbf {B} }{\displaystyle \mathbf {A} \cdot \mathbf {B} } são dadas por

A i j ... k ℓ ... B m n ... p ... i = ∑ i = 1 n A i j ... k ℓ ... B m n ... p ... i {\i1}displaystyle A_{\i}dots B_B_{mn}dots {p{dots }i}=sum _{i=1}{n}A_{ij{ij}dots {k}dots {k}ell B_B_{mn}dots {mn}dots {p{dots }i} {\displaystyle A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}}

Esta definição reduz naturalmente ao produto vetorial padrão ponto quando aplicado a vetores, e multiplicação de matrizes quando aplicado a matrizes.

Ocasionalmente, um produto de ponto duplo é usado para representar a multiplicação e a soma através de dois índices. O produto de ponto duplo entre dois tensores de segunda ordem é um escalar.

Páginas relacionadas

 

Perguntas e Respostas

P: O que é o produto escalar em matemática?


R: O produto escalar é uma operação que recebe dois vetores como entrada e retorna um número escalar como saída.

P: De que depende o produto escalar?


R: O produto escalar depende do comprimento de ambos os vetores e do ângulo entre eles.

P: Por que o nome do produto escalar é derivado do ponto centralizado "-"?


R: O nome é derivado do ponto centralizado "-", que é frequentemente usado para designar essa operação.

P: Qual é o nome alternativo para o produto escalar?


R: O nome alternativo é produto escalar, que enfatiza a natureza escalar (em vez de vetorial) do resultado.

P: Qual é o contraste entre o produto escalar e o produto vetorial no espaço tridimensional?


R: O produto escalar produz um número escalar como resultado, enquanto o produto vetorial produz um vetor como resultado.

P: Para que é usado o produto escalar na matemática?


R: O produto escalar pode ser usado para determinar se dois vetores são perpendiculares (têm um ângulo de 90 graus) e para projetar um vetor em outro.

P: O produto escalar pode ser usado em espaços de dimensões maiores?


R: Sim, o produto escalar pode ser estendido a espaços de dimensões maiores, generalizando a definição.

AlegsaOnline.com - 2020 / 2023 - License CC3