Transformada de Fourier

A transformação de Fourier é uma função matemática que pode ser utilizada para encontrar as frequências de base que compõem um sinal ou onda. Por exemplo, se um acorde for tocado, a onda sonora do acorde pode ser introduzida numa transformada de Fourier para encontrar as notas a partir das quais o acorde é feito. A saída de uma transformada de Fourier é por vezes chamada um espectro ou distribuição de frequências porque apresenta um espectro das frequências da entrada. Esta função tem muitos usos na criptografia, oceanografia, aprendizagem de máquinas, radiologia, física quântica, bem como na concepção e visualização de som.

A transformação de Fourier de uma função f ( x ) f(x)} f(x) é dada por

F ( α ) = ∫ - ∞ + ∞ f ( x ) e - 2 π i α x d x {\i1}displaystyle F({\i}alpha )=int _{\i1}f(x)e^{-2\i i}alpha x}dx} $F(\alpha )=\int _{-\infty }^{+\infty }f(x)e^{-2\pi i\alpha x}dx$

F ( α ) F(alfa ) $F(\alpha )$ é a função transformadora de Fourier e retorna um valor que representa a frequência prevalecente α {\displaystyle F(alfa ) $\alpha$ está no sinal original.

e - 2 π i α x ^{\i i i}displaystyle e^{-2\i i}alpha x}} $e^{-2\pi i\alpha x}$ Representa o embrulho da função de entrada f ( x ) f(x)} f(x) em torno da origem no plano complexo com alguma frequência α {\i1}displaystyle {\i} $\alpha$

A transformação inversa de Fourier é dada por

f ( x ) = ∫ - ∞ + ∞ F ( α ) e + 2 π i x α d α {\i1}displaystyle f(x)=int _{\i}{+\i}f({\i}alpha )e^{+2\i ix\i ix\i}dalpha {\i} $f(x)=\int _{-\infty }^{+\infty }F(\alpha )e^{+2\pi ix\alpha }d\alpha$

Uma transformação de Fourier mostra quais são as frequências de um sinal. Por exemplo, considere uma onda sonora que contém três notas musicais diferentes: A, B, e C. Fazer um gráfico da transformação de Fourier desta onda sonora (com a frequência no eixo x e a intensidade no eixo y) mostrará um pico em cada frequência que corresponde a uma das notas musicais.

Muitos sinais podem ser criados pela soma de co-senos e pecados com amplitudes e frequências variáveis. A transformada de Fourier traça as amplitudes e fases destes cossenos e pecados contra as suas respectivas frequências.

As transformações de Fourier são importantes porque muitos sinais fazem mais sentido quando as suas frequências são separadas. No exemplo de áudio acima, olhar para o sinal com respeito ao tempo não torna óbvio que as notas A, B, e C estão no sinal. Muitos sistemas fazem coisas diferentes a frequências diferentes, pelo que estes tipos de sistemas podem ser descritos pelo que fazem a cada frequência. Um exemplo disto é um filtro que bloqueia frequências altas.

O cálculo de uma transformação de Fourier requer a compreensão da integração e números imaginários. Os computadores são normalmente utilizados para calcular transformadas de Fourier de tudo menos os sinais mais simples. A Transformada Rápida de Fourier é um método que os computadores utilizam para calcular rapidamente uma transformação de Fourier.

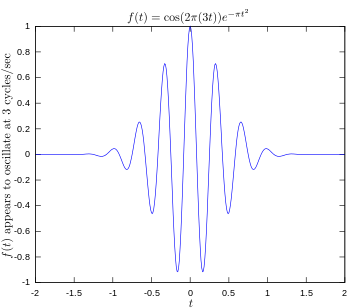
Função original mostrando um sinal oscilante a 3 hertz.

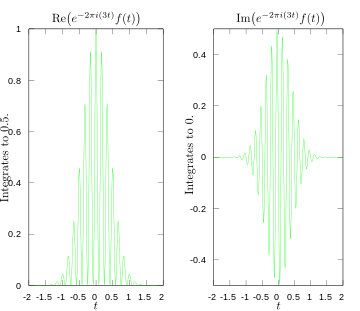
Partes reais e imaginárias da integração e para a transformação de Fourier a 3 hertz

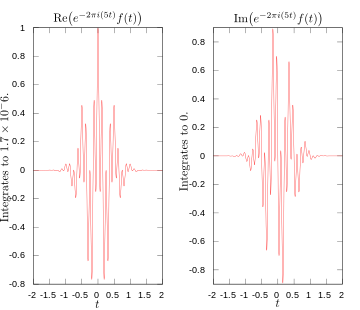
Partes reais e imaginárias da integração e para a transformação de Fourier a 5 hertz

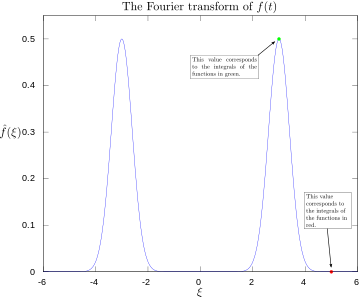
Transformada de Fourier com 3 e 5 hertz etiquetada.

Perguntas e Respostas

P: O que é a transformação de Fourier?

R: A transformada de Fourier é uma função matemática que pode ser usada para encontrar as freqüências de base de que uma onda é feita. Ela pega uma onda complexa e encontra as freqüências que a compõem, permitindo-lhe identificar as notas que compõem um acorde.

P: Quais são alguns usos da transformada de Fourier?

R: A transformação de Fourier tem muitos usos em criptografia, oceanografia, aprendizado de máquina, radiologia, física quântica, bem como desenho e visualização de som.

P: Como é calculada a transformada de Fourier?

R: A transformada de Fourier de uma função f(x) é dada por F(ב) = ∫-∞+∞f(x)e-2נiבxdx onde ב é uma freqüência. Isso retorna um valor que representa o quão prevalecente é a frequência ב no sinal original. A transformação inversa de Fourier é dada por f(x) = ∫-∞+∞F(ב)e+2נixבdב.

P: Como é a saída de uma transformada de Fourier?

R: Uma saída de uma Transformada de Fourier pode ser chamada de espectro de freqüência ou distribuição, porque mostra uma distribuição de possíveis freqüências da entrada.

P: Como os computadores calculam as Transformadas rápidas de Fourier?

R: Os computadores usam um algoritmo chamado Transformada Rápida de Fourier (FFT) para calcular rapidamente quaisquer transformações de sinais, exceto as mais simples.

P: O que não nos mostra a análise dos sinais com relação ao tempo?

R: Olhar os sinais com relação ao tempo não faz com que seja óbvio que notas estão presentes neles; muitos sinais fazem mais sentido quando suas freqüências são separadas e analisadas individualmente.