Séries harmônicas (matemática)

Em matemática, a série harmônica é a divergente série infinita:

∑ n = 1 ∞ 1 n = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\i1}{\i1}}{\i1}}frac {\i1}=1+{\i1}1+{\i1}frac {\i}{\i}+{\i1}{\i1}+{\i}frac {\i}{\i1}{\i}+{\i}frac {\i}{\i}{\i1}{\i1}+{\i}frac {\i}{\i}}{\i1}}frac $\sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

Divergente significa que à medida que você acrescenta mais termos, a soma nunca deixa de aumentar. Ela não vai em direção a um único valor finito.

Infinito significa que você pode sempre acrescentar outro termo. Não há um termo final para a série.

Seu nome vem da idéia de harmônicas na música: os comprimentos de onda dos sobre-tons de uma corda vibratória são 1/2, 1/3, 1/4, etc., do comprimento de onda fundamental da corda. Além do primeiro termo, cada termo da série é a média harmônica dos termos de cada lado da mesma. A frase média harmônica também vem da música.

História

O fato de a série harmônica divergir foi comprovado pela primeira vez no século XIV por Nicole Oresme, mas foi esquecido. As provas foram dadas no século XVII por Pietro Mengoli, Johann Bernoulli e Jacob Bernoulli.

Seqüências harmônicas têm sido utilizadas por arquitetos. No período barroco os arquitetos as utilizaram nas proporções de plantas baixas, elevações e nas relações entre detalhes arquitetônicos de igrejas e palácios.

Divergência

Existem várias provas bem conhecidas da divergência da série harmônica. Algumas delas são dadas abaixo.

Teste comparativo

Uma maneira de provar a divergência é comparar a série harmônica com outra série divergente, onde cada denominador é substituído pela potência seguinte, a maior de duas:

1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {\displaystyle {\begin{\alinhado}&1 + 1 + 1 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 16 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 9 + 1 8 + 1 8 + 1 8 + 1 81+frac 1+frac 2+frac 1+frac 1+cores 4+mathbf +frac 1 +frac 1 +frac 1 cor +frac 1 cor +frac 1 cor +frac 1 +frac 1 +frac 1 cor +cdots end{alinhados} ${\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16} }}}+\cdots \end{aligned}}$

Cada termo da série harmônica é maior ou igual ao termo correspondente da segunda série, e portanto a soma da série harmônica deve ser maior ou igual à soma da segunda série. Entretanto, a soma da segunda série é infinita:

1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + 1 2 + 1 2 + ⋯ = ∞ {\i1}{\i1}{\i1}esquerda(1) + esquerda(2)(1) + esquerda(1)(4)!+\Direita!+\esquerda (1)!Frrac 1 16 direita + pontos + pontos + 12pt = 1 + 1 + Frrac 1 + 2 + Frrac 1 + 2 + 2 + Frrac 1 + 2 + 1 + 2 pontos + 1 + 1 + 2 pontos = 1 + 1 ${\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}$

Segue-se (pelo teste de comparação) que a soma das séries harmônicas também deve ser infinita. Mais precisamente, a comparação acima prova que

∑ n = 1 2 k 1 n ≥ 1 + k 2 {\i1}sum _{n=1}^{2^{k}}{frac {1}{n}}geq 1+{frac {k}{2}}} $\sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}$

para cada número inteiro positivo $k$ .

Esta prova, proposta por Nicole Oresme por volta de 1350, é considerada como um ponto alto da matemática medieval. É ainda hoje uma prova padrão ensinada nas aulas de matemática.

Teste integral

É possível provar que a série harmônica diverge ao comparar sua soma com uma integral imprópria. Considere a disposição dos retângulos mostrados na figura à direita. Cada retângulo tem 1 unidade de largura e 1 unidade de altura, portanto, a área total do número infinito de retângulos é a soma da série harmônica:

área de retângulos = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ ${\begin{array}{c}{\text{area of}}\\{\text{rectangles}}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

A área total sob a curva $y =$ 1/x de 1 até o infinito é dada por um integral impróprio divergente:

área sob curva = ∫ 1 ∞ 1 x d x = ∞ . estilo de jogo c/ área de texto em curva } ${\begin{array}{c}{\text{area under}}\\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty .$

Como esta área está inteiramente contida dentro dos retângulos, a área total dos retângulos também deve ser infinita. Isto prova que

∑ n = 1 k 1 n > ∫ 1 k + 1 1 1 x d x = ln ( k + 1 ) . estilo de jogo _{n=1}{k}{frac {1}{n}>int _{1}^{k+1}{frac {1}{x}},dx=ln(k+1). } $\sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1).$

A generalização deste argumento é conhecida como o teste integral.

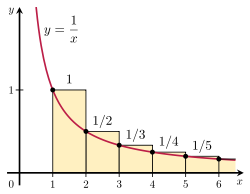
Ilustração do teste integral.

Taxa de divergência

As séries harmônicas divergem muito lentamente. Por exemplo, a soma dos primeiros 1043 termos é inferior a 100. Isto porque as somas parciais das séries têm um crescimento logarítmico. Em particular, a série harmônica é muito diferente,

∑ n = 1 k 1 n = ln k + γ + ε k ≤ ( ln k ) + 1 {\i1}{\i1}^{\i}{\i1}frac {\i}=ln k+\i}gamma +\i}varepsilon _{\i}leq (n k)+1} $\sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1$

onde $γ$ é a constante Euler-Mascheroni e $εk ~$ 1/2k que se aproxima de 0 como $k$ vai ao infinito. Leonhard Euler provou tanto isto como também que a soma que inclui apenas os recíprocos dos primes também diverge, ou seja:

∑ p prime 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ . estilo de jogo _{\i1}{\i1}={\i1}{\i1}+{\i1}frac {\i}{\i1}{\i1}{\i1}+{\i}frac {\i}{\i1}{\i1}{\i1}+{\i1}{\i1}+{\i}frac {\i}{\i1}{\i1}+{\i1}{\i1}+{\i1}{\i1}+frac {\i}{\i}{\i1}{17}+cdots =infty . } $\sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .$

Somas parciais

Os primeiros trinta números harmônicos
$n$	Soma parcial da série harmônica, $Hn$
$n$	expresso como uma fração		decimal	tamanho relativo
1	1		~1	1
2	3	/2	~1.5	1.5
3	11	/6	~1.83333	1.83333
4	25	/12	~2.08333	2.08333
5	137	/60	~2.28333	2.28333
6	49	/20	~2.45	2.45
7	363	/140	~2.59286	2.59286
8	761	/280	~2.71786	2.71786
9	7129	/2520	~2.82897	2.82897
10	7381	/2520	~2.92897	2.92897
11	83711	/27720	~3.01988	3.01988
12	86021	/27720	~3.10321	3.10321
13	1145993	/360360	~3.18013	3.18013
14	1171733	/360360	~3.25156	3.25156
15	1195757	/360360	~3.31823	3.31823
16	2436559	/720720	~3.38073	3.38073
17	42142223	/12252240	~3.43955	3.43955
18	14274301	/4084080	~3.49511	3.49511
19	275295799	/77597520	~3.54774	3.54774
20	55835135	/15519504	~3.59774	3.59774
21	18858053	/5173168	~3.64536	3.64536
22	19093197	/5173168	~3.69081	3.69081
23	444316699	/118982864	~3.73429	3.73429
24	1347822955	/356948592	~3.77596	3.77596
25	34052522467	/8923714800	~3.81596	3.81596
26	34395742267	/8923714800	~3.85442	3.85442
27	312536252003	/80313433200	~3.89146	3.89146
28	315404588903	/80313433200	~3.92717	3.92717
29	9227046511387	/2329089562800	~3.96165	3.96165
30	9304682830147	/2329089562800	~3.99499	3.99499

As somas parciais finitas das séries harmônicas divergentes,

H n = ∑ k = 1 n 1 k , {\i1}{\i1}sum _{\i=1}^{\i}{\i}{\i}{\i1},} $H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},$

são chamados de números harmônicos.

A diferença entre $Hn$ e $ln n$ converge para a constante Euler-Mascheroni. A diferença entre quaisquer dois números harmônicos nunca é um número inteiro. Nenhum número harmônico é um número inteiro, exceto para $H1 = 1$ .

Séries relacionadas

Séries harmônicas alternadas

A série

∑ n = 1 ∞ ( - 1 ) n + 1 n = 1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ {\i1}- estilo de exibição {\i}{\i1}{\i1}-{\i1}-frac {\i}{\i}{\i}=1-{\i}+{\i}frac {\i}{\i}{\i1}-{\i}-{\i1}{\i1}+{\i}frac {\i}{\i}{\i}- 5 pontos $\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots$

é conhecida como a série harmônica alternada. Esta série converge através do teste de série alternada. Em particular, a soma é igual ao logaritmo natural de 2:

1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ = ln 2. estilo de jogo 1-frac {1}{2}+frac {1}-{3}-frac {1}{4}+frac {5}-cdots =ln 2.} $1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.$

A série harmônica alternada, embora condicionalmente convergente, não é absolutamente convergente: se os termos da série são sistematicamente reordenados, em geral a soma torna-se diferente e, dependendo da reordenação, possivelmente até infinita.

A fórmula da série harmônica alternada é um caso especial da série Mercator, a série Taylor para o logaritmo natural.

Uma série relacionada pode ser derivada da série Taylor para o arctangent:

∑ n = 0 ∞ ( - 1 ) n 2 n + 1 = 1 - 1 3 + 1 5 - 1 7 + ⋯ = π 4 . } $\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}.$

Esta é conhecida como a série Leibniz.

Série harmônica geral

A série harmônica geral é da forma

∑ n = 0 ∞ 1 a n + b , {\i1}displaystyle {\i}sum _{\i=0}^^{\i}{\i1}frac {\i}{an+b},} $\sum _{n=0}^{\infty }{\frac {1}{an+b}},$

onde $a \neq 0$ e $b$ são números reais, e b/a não é zero ou um número inteiro negativo.

Pelo teste de comparação de limites com as séries harmônicas, todas as séries harmônicas gerais também divergem.

$série p$

Uma generalização da série harmônica é a $série p$ (ou série hiper-harmônica), definida como

∑ n = 1 ∞ 1 n p {\i1}sum _{n=1}^{\i1}frac {n^{p}}}} $\sum _{n=1}^{\infty }{\frac {1}{n^{p}}}$

para qualquer número real $p$ . Quando $p = 1$ , a $série p$ é a série harmônica, que diverge. Ou o teste integral ou o teste de condensação Cauchy mostra que a $série p$ converge para todos os $p > 1 ($ neste caso, é chamada de série sobre-harmônica) e diverge para todos os p $\leq 1.$ Se $p > 1$ então a soma da série p é ζ( $p), ou seja,$ a função zeta Riemann avaliada em p.

O problema de encontrar a soma para $p = 2$ é chamado de problema da Basiléia; Leonhard Euler mostrou que é ^π2/6. O valor da soma para $p = 3$ é chamado de constante de Apéry, já que Roger Apéry provou que se trata de um número irracional.

ln-series

Relacionada com a $série p$ é a série ln, definida como

∑ n = 2 ∞ 1 n ( ln n ) p {\i1}displaystyle {\i=2}^{\i}{\i1}frac {\i}{n(\i n)^{p}}}} $\sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}$

para qualquer número real positivo $p.$ Isto pode ser demonstrado pelo teste integral para divergir para $p \leq 1$ , mas convergir para todos $p > 1.$

$Série φ$

Para qualquer função convexa, de valor real $φ$ tal que

lim sup u → 0 + φ ( u 2 ) φ ( u ) < 1 2 , estilo de jogo _{u}{\i}{\i1}{\i}{\i1}frac {\i}{\i1}-esquerda(u){\i}(u){\i}{\i1}-varphi(u){\i}(u){\i}{\i1}(u){\i}-direita $\limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}},$

a série

∑ n = 1 ∞ φ ( 1 n ) {\i} {\i1}displaystyle {\i}sum _{\i=1}^{\i1}varphi {\i}left(frac {\i}{\i1}right){\i} $\sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)$

é convergente. ^[]

Série harmônica aleatória

A série harmônica aleatória

∑ n = 1 ∞ s n n , {\i1}displaystyle {n=1}^{\i}{\i1}frac {s_n}, {n},} $\sum _{n=1}^{\infty }{\frac {s_{n}}{n}},$

onde as $sn$ são variáveis aleatórias independentes, distribuídas de forma idêntica tomando os valores +1 e -1 com igual probabilidade 1/2, é um exemplo bem conhecido na teoria da probabilidade para uma série de variáveis aleatórias que convergem com a probabilidade 1. O fato desta convergência é uma consequência fácil tanto do teorema de Kolmogorov de três séries quanto da desigualdade máxima de Kolmogorov intimamente relacionada. Byron Schmuland da Universidade de Alberta examinou mais detalhadamente as propriedades da série harmônica aleatória e mostrou que a série convergente é uma variável aleatória com algumas propriedades interessantes. Em particular, a função de densidade de probabilidade desta variável aleatória avaliada em +2 ou em -2 assume o valor 0,12499999999999999999999999999999999999764..., diferindo de 1/8 por menos de 10-42. O trabalho de Schmuland explica porque esta probabilidade é tão próxima, mas não exatamente, de 1/8. O valor exato desta probabilidade é dado pelo produto cosseno integral infinito $C2$ dividido por π.

Séries harmônicas esgotadas

A série harmônica esgotada onde todos os termos em que o dígito 9 aparece em qualquer lugar do denominador são removidos pode ser mostrada para convergir e seu valor é inferior a 80. De fato, quando todos os termos contendo qualquer seqüência de dígitos em particular (em qualquer base) são removidos, a série converge.

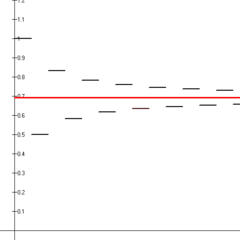
As primeiras catorze somas parciais da série harmônica alternada (segmentos de linha preta) mostradas convergindo para o logaritmo natural de 2 (linha vermelha).

Aplicações

A série harmônica pode ser contraintuitiva. Isto porque é uma série divergente, mesmo que os termos da série fiquem menores e vão para zero. A divergência da série harmônica é a fonte de alguns paradoxos.

A "minhoca no elástico". Suponha que uma minhoca se arraste ao longo de um elástico infinito de um metro de elástico ao mesmo tempo em que o elástico é esticado uniformemente. Se a minhoca percorrer 1 centímetro por minuto e o elástico esticar 1 metro por minuto, a minhoca chegará alguma vez ao fim do elástico? A resposta, contraintuitivamente, é "sim", pois após $n$ minutos, a relação entre a distância percorrida pelo verme e o comprimento total do elástico é

1 100 ∑ k = 1 n 1 k . } ${\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}.$

Como a série fica arbitrariamente grande à medida que $n$ se torna maior, eventualmente esta proporção deve exceder 1, o que implica que o verme atinge o fim do elástico. Entretanto, o valor de $n$ em que isso ocorre deve ser extremamente grande: aproximadamente e100, um número superior a 1043 minutos (1037 anos). Embora a série harmônica divirja, ela o faz muito lentamente.

O problema do jipe pergunta quanto combustível total é necessário para um carro com uma capacidade limitada de transporte de combustível para atravessar um deserto, deixando quedas de combustível ao longo da rota. A distância que o carro pode percorrer com uma determinada quantidade de combustível está relacionada às somas parciais da série harmônica, que crescem logaritmicamente. E assim o combustível necessário aumenta exponencialmente com a distância desejada.

O problema do empilhamento de blocos: dado um conjunto de dominós idênticos, é possível empilhá-los na borda de uma mesa para que fiquem pendurados sobre a borda da mesa sem cair. O resultado contraintuitivo é que eles podem ser empilhados de forma que a saliência seja tão grande quanto você desejar. Isto é, desde que haja dominós suficientes.

Um nadador que vai mais rápido cada vez que eles tocam a parede da piscina. O nadador começa a atravessar uma piscina de 10 metros a uma velocidade de 2 m/s, e a cada travessia, outros 2 m/s são adicionados à velocidade. Em teoria, a velocidade do nadador é ilimitada, mas o número de cruzes da piscina necessárias para chegar a essa velocidade torna-se muito grande; por exemplo, para chegar à velocidade da luz (ignorando a relatividade especial), o nadador precisa atravessar a piscina 150 milhões de vezes. Ao contrário deste grande número, o tempo necessário para atingir uma determinada velocidade depende da soma das séries em qualquer número determinado de cruzes da piscina:

10 2 ∑ k = 1 n 1 k . estilo de jogo 10frac } ${\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}.$

O cálculo da soma mostra que o tempo necessário para chegar à velocidade da luz é de apenas 97 segundos.

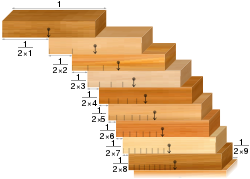
O problema de empilhamento de blocos: blocos alinhados de acordo com as clivagens de pontes em série harmônica de qualquer largura.

Páginas relacionadas

Progressão harmônica
Lista de somas de reciprocidade

Perguntas e Respostas

P: O que é a série harmônica?

R: A série harmônica é uma série infinitamente divergente onde cada termo é igual a 1 dividido por sua posição na seqüência.

P: O que significa para uma série ser divergente?

R: Divergente significa que, ao acrescentar mais termos, a soma nunca deixa de aumentar e não vai em direção a um único valor finito.

P: O que significa para uma série ser infinita?

R: Infinito significa que o senhor sempre pode acrescentar outro termo e que não há um termo final para a série.

P: De onde vem o nome dessa série?

R: O nome desta série vem da idéia de harmônicas na música, onde os comprimentos de onda dos sobre-tons são 1/2, 1/3, 1/4, etc., do comprimento de onda fundamental da corda.

P: O que é um meio harmônico?

R: Uma média harmônica é quando cada termo em uma seqüência é igual à média harmônica de seus termos vizinhos. Essa frase também vem da música.

P: Como calculamos cada termo nesta seqüência?

R: Cada termo nesta seqüência pode ser calculado dividindo um pela sua posição na seqüência (1/n).