Integral de superfície

Em matemática, uma integral de superfície é uma integral definitiva tomada sobre uma superfície (que pode ser uma curva definida no espaço). Assim como uma integral de linha lida com uma dimensão ou uma variável, uma integral de superfície pode ser pensada como sendo uma integral dupla ao longo de duas dimensões. Dada uma superfície, pode-se integrar sobre seus campos escalares (ou seja, funções que retornam números como valores), e campos vetoriais (ou seja, funções que retornam vetores como valores).

As integrais de superfície têm aplicações na física, particularmente com a teoria clássica do eletromagnetismo.

A definição de superfície integral depende da divisão da superfície em pequenos elementos de superfície.

Uma ilustração de um único elemento de superfície. Estes elementos são feitos infinitamente pequenos, pelo processo limitador, de modo a se aproximar da superfície.

Integrais superficiais de campos escalares

Considere uma superfície S na qual um campo escalar f é definido. Se pensarmos em S como sendo feito de algum material, e para cada x em S o número f(x) é a densidade do material em x, então a integral da superfície de f sobre S é a massa por unidade de espessura de S. (Isto só é verdade se a superfície for uma casca infinitesimalmente fina.) Uma abordagem para calcular a superfície integral é então dividir a superfície em muitas peças muito pequenas, assumir que em cada peça a densidade é aproximadamente constante, encontrar a massa por unidade de espessura de cada peça multiplicando a densidade da peça por sua área, e então somar os números resultantes para encontrar a massa total por unidade de espessura de S.

Para encontrar uma fórmula explícita para a integral de superfície, os matemáticos parametrizam S considerando em S um sistema de coordenadas curvilíneas, como a latitude e longitude em uma esfera. Que tal parametrização seja x(s, t), onde (s, t) varia em alguma região T no plano. Então, a integral da superfície é dada por

∫ S f d S = ∬ T f ( x ( s , t ) ) | ∂ x ∂ s × ∂ x ∂ t | d s d t |displaystyle |int _{S}f\,dS=iint _{T}f(|mathbf {x} (s,t))esquerda \em parte, em parte, em parte, em parte, em parte, em parte, em parte \em parte, certo, dt...} $\int _{S}f\,dS=\iint _{T}f(\mathbf {x} (s,t))\left|{\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right|ds\,dt$

onde a expressão entre barras do lado direito é a magnitude do produto cruzado dos derivados parciais de x(s, t).

Por exemplo, para encontrar a área de superfície de alguma forma funcional geral, digamos z = f ( x , y ) {\displaystyle z=f\,(x,y)} $z=f\,(x,y)$ temos

A = ∫ S d S = ∬ T ‖ ∂ r ∂ x × ∂ r ∂ y ‖ d x d y {\i1}displaystyle A=int _{\i},dS=iint _{\i}{\i1}esquerda _{\i}{\i1}parcial \em parte x em parte x em parte \em parte sim, em parte sim, em parte sim...} $A=\int _{S}\,dS=\iint _{T}\left\|{\partial \mathbf {r} \over \partial x}\times {\partial \mathbf {r} \over \partial y}\right\|dx\,dy$

onde r = ( x , y , z ) = ( x , y , f ( x , y ) ) {\i1}displaystyle {r} =(x,y,z)=(x,y,f(x,y))} $\mathbf {r} =(x,y,z)=(x,y,f(x,y))$ . De modo que ∂ r ∂ x = ( 1 , 0 , f x ( x , y ) ) estilo de jogo parcial \{x}(1,0,f_{x}(x,y))} ${\partial \mathbf {r} \over \partial x}=(1,0,f_{x}(x,y))$ , e ∂ r ∂ y = ( 0 , 1 , f y ( x , y ) ) estilo de jogo parcial \em parte y}=(0,1,f_{y}(x,y))} ${\partial \mathbf {r} \over \partial y}=(0,1,f_{y}(x,y))$ . Então,

A = ∬ T ‖ ( 1 , 0 , ∂ f ∂ x ) × ( 0 , 1 , ∂ f ∂ y ) ‖ d x d y = ∬ T ‖ ( - ∂ f ∂ x , - ∂ f ∂ y , 1 ) ‖ d x d y = ∬ T ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 + 1 d x d y {\i1}a&Esquerda(1,0,0,parcial para esquerda(1,0,0,parcial para a direita) vezes esquerda(0,1,parcial para a direita) direita(0,1,parcial para a direita) direita(0,1,parcial para a direita) direita(0,0,0,parcial para a direita)esquerda esquerda (-parcial para esquerda), -parcial para esquerda (-parcial para cima), -parcial para cima (-parcial para cima), 1 direita), direita (-dx), direita (-dx), esquerda (-dx), direita (-dx)esquerda, esquerda, direita, direita, esquerda, direita, direita, esquerda, direita ${\begin{aligned}A&{}=\iint _{T}\left\|\left(1,0,{\partial f \over \partial x}\right)\times \left(0,1,{\partial f \over \partial y}\right)\right\|dx\,dy\\&{}=\iint _{T}\left\|\left(-{\partial f \over \partial x},-{\partial f \over \partial y},1\right)\right\|dx\,dy\\&{}=\iint _{T}{\sqrt {\left({\partial f \over \partial x}\right)^{2}+\left({\partial f \over \partial y}\right)^{2}+1}}\,\,dx\,dy\end{aligned}}$

que é a fórmula utilizada para a área de superfície de uma forma funcional geral. Pode-se reconhecer o vetor na segunda linha acima como o vetor normal para a superfície.

Observe que devido à presença do produto cruzado, as fórmulas acima só funcionam para superfícies embutidas em espaço tridimensional.

Integrais superficiais de campos vetoriais

Considere um campo vetorial v em S, ou seja, para cada x em S, v(x) é um vetor.

A integral de superfície pode ser definida como componente de acordo com a definição da integral de superfície de um campo escalar; o resultado é um vetor. Por exemplo, isto se aplica ao campo elétrico em algum ponto fixo devido a uma superfície com carga elétrica, ou à gravidade em algum ponto fixo devido a uma folha de material. Também pode calcular o fluxo magnético através de uma superfície.

Alternativamente, os matemáticos podem integrar o componente normal do campo vetorial; o resultado é um escalar. Um exemplo é um fluido que flui através de S, tal que v(x) determina a velocidade do fluido em x. O fluxo é definido como a quantidade de fluido que flui através de S em uma unidade de tempo.

Esta ilustração implica que se o campo vetorial é tangente a S em cada ponto, então o fluxo é zero, porque o fluido flui em paralelo a S, e nem entra nem sai. Isto também implica que se v não flui apenas ao longo de S, ou seja, se v tem tanto um componente tangencial quanto um normal, então apenas o componente normal contribui para o fluxo. Com base neste raciocínio, para encontrar o fluxo, precisamos levar o produto ponto de v com a superfície da unidade normal para S em cada ponto, o que nos dará um campo escalar, e integrar o campo obtido como acima. Isto nos dá a fórmula

∫ S v ⋅ d S = ∫ S ( v ⋅ n ) d S = ∬ T v ( x ( s , t ) ) ⋅ ( ∂ x ∂ s × ∂ x ∂ t ) d s d t . d d d d d d d d d d d d d d d d d d d d d d d d Não sei... (s,t))cdot(s,t)(s,t)(s,t)(s) \em parte, em parte, em parte, em parte, em parte, em parte, em parte \em parte, certo)ds,dt. } $\int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }=\int _{S}({\mathbf {v} }\cdot {\mathbf {n} })\,dS=\iint _{T}{\mathbf {v} }(\mathbf {x} (s,t))\cdot \left({\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right)ds\,dt.$

O produto cruzado no lado direito desta expressão é uma superfície normal determinada pela parametrização.

Esta fórmula define o integral à esquerda (note o ponto e a notação vetorial para o elemento de superfície).

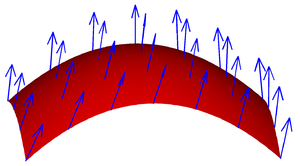
Um campo vetorial em uma superfície.

Teoremas que envolvem integrais de superfície

Vários resultados úteis para integrais de superfície podem ser derivados usando geometria diferencial e cálculo vetorial, como o teorema da divergência, e sua generalização, o teorema de Stokes.

Questões avançadas

Mudança de parametrização

A discussão acima definiu a superfície integral utilizando uma parametrização da superfície S. Uma determinada superfície pode ter várias parametrizações. Por exemplo, quando as localizações do Pólo Norte e Pólo Sul são movidas em uma esfera, a latitude e a longitude mudam para todos os pontos da esfera. Uma questão natural é, então, se a definição da integral da superfície depende da parametrização escolhida. Para integrais de campos escalares, a resposta a esta pergunta é simples, o valor da integral de superfície será o mesmo, não importa qual parametrização se utilize.

Os integrais dos campos vetoriais são mais complicados, porque a superfície normal está envolvida. Os matemáticos provaram que, dadas duas parametrizações da mesma superfície, cujas normas de superfície apontam na mesma direção, ambas as parametrizações dão o mesmo valor para a integral da superfície. Se, entretanto, as normas para estas parametrizações apontam em direções opostas, o valor da integral de superfície obtido usando uma parametrização é o negativo de uma obtida através da outra parametrização. Segue-se que, dada uma superfície, não precisamos nos ater a nenhuma parametrização única; mas, ao integrar campos vetoriais, precisamos decidir antecipadamente para qual direção a normal apontará e então escolher qualquer parametrização consistente com aquela direção.

As parametrizações funcionam em partes da superfície

Outra questão é que às vezes as superfícies não têm parametrizações que cobrem toda a superfície; isto é verdade, por exemplo, para a superfície de um cilindro (de altura finita). A solução óbvia é então dividir essa superfície em várias peças, calcular a superfície integral em cada peça, e depois somá-las todas. De fato, é assim que as coisas funcionam, mas ao integrar campos vetoriais, é preciso ter cuidado novamente com a escolha do vetor de ponta normal para cada peça da superfície, para que, quando as peças forem colocadas novamente juntas, os resultados sejam consistentes. Para o cilindro, isto significa que se decidirmos que para a região lateral o normal apontará para fora do corpo, então para as partes circulares superior e inferior o normal deve apontar para fora do corpo também.

Normas de superfície inconsistentes

Finalmente, existem superfícies que não têm uma superfície normal em cada ponto com resultados consistentes (por exemplo, a faixa de Möbius). Se tal superfície for dividida em peças, em cada peça é escolhida uma parametrização e a superfície correspondente normal, e as peças são novamente colocadas juntas, os vetores normais provenientes de peças diferentes não podem ser reconciliados. Isto significa que em alguma junção entre duas peças, os vetores normais apontam em direções opostas. Tal superfície é chamada de não-orientável. Os campos vetoriais não podem ser integrados em superfícies não-orientadas.

Páginas relacionadas

Teorema da divergência
Teorema de Stokes
Linha integral
Volume integral
Sistema de coordenadas cartesianas
Elementos de volume e área de superfície em um sistema de coordenadas esféricas
Elementos de volume e área de superfície em um sistema de coordenadas cilíndricas
Método Holstein - arenque