Espaço-Tempo
O espaço-tempo é um modelo matemático que une espaço e tempo em uma única idéia chamada continuum. Este continuum tetradimensional é conhecido como espaço Minkowski.
A combinação destas duas idéias ajudou a cosmologia a entender como o universo funciona no nível grande (por exemplo, galáxias) e no nível pequeno (por exemplo, átomos).
Na mecânica clássica não-relativista, o uso do espaço euclidiano em vez do espaço-tempo é bom, porque o tempo é tratado como universal com uma taxa de passagem constante que é independente do estado de movimento de um observador.
Mas em um universo relativista, o tempo não pode ser separado das três dimensões do espaço. Isto porque a taxa observada em que o tempo passa depende da velocidade de um objeto em relação ao observador. Além disso, a força de qualquer campo gravitacional retarda a passagem do tempo para um objeto como visto por um observador fora do campo.
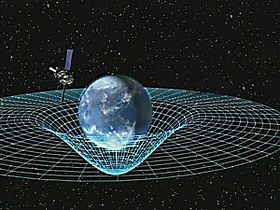
Uma ilustração da curvatura espaço-tempo causada pela Terra.
Outros aspectos
Onde quer que exista matéria, ela dobra a geometria do espaço-tempo. Isto resulta em uma forma curva do espaço-tempo que pode ser entendida como gravidade. As linhas brancas na imagem à direita representam o efeito da massa sobre o espaço-tempo.
Na mecânica clássica, o uso do tempo espacial é opcional, já que o tempo é independente do movimento nas três dimensões do espaço euclidiano. Entretanto, quando um corpo se move a velocidades próximas à velocidade da luz (velocidades relativistas), o tempo não pode ser separado das três dimensões do espaço. O tempo, do ponto de vista de um observador estacionário, depende de quão próximo da velocidade da luz o objeto está se movendo.
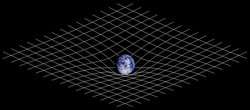
Analogia bidimensional da distorção espaço-tempo
Origem histórica
Muitas pessoas ligam o espaço-tempo a Albert Einstein, que propôs uma relatividade especial em 1905. Entretanto, foi o professor de Einstein, Hermann Minkowski, que sugeriu o espaço-tempo, em um ensaio de 1908. Seu conceito de espaço Minkowski é o mais antigo tratamento do espaço e do tempo como dois aspectos de um todo unificado, que é a essência da relatividade especial. Ele esperava que esta nova idéia esclarecesse a teoria da relatividade especial.
O espaço-tempo Minkowski só é preciso para descrever a velocidade constante. Foi Einstein, porém, quem descobriu a curvatura do espaço-tempo (gravidade) na relatividade geral. Na relatividade geral, Einstein generalizou o espaço-tempo de Minkowski para incluir os efeitos da aceleração. Einstein descobriu que a curvatura em sua representação espaço-tempo 4-dimensional era na verdade a causa da gravidade.
A décima terceira edição da Encyclopedia Britannica de 1926 incluiu um artigo de Einstein intitulado "espaço-tempo".
Antecedentes literários
Edgar Allan Poe escreveu um ensaio sobre cosmologia intitulado Eureka (1848), que dizia que "espaço e duração são um só". Esta é a primeira instância conhecida de sugerir que o espaço e o tempo são percepções diferentes de uma coisa. Poe chegou a esta conclusão após aproximadamente 90 páginas de raciocínio, mas não empregou nenhuma matemática.
Em 1895, H. G. Wells em seu romance, A Máquina do Tempo, escreveu: "Não há diferença entre o Tempo e qualquer uma das três dimensões do Espaço, exceto que nossa consciência se move ao longo dele". Ele acrescentou: "As pessoas científicas... sabem muito bem que o Tempo é apenas uma espécie de Espaço".
Tempo de espaço na mecânica quântica
Na relatividade geral, o espaço-tempo é pensado como suave e contínuo. No entanto, na teoria da mecânica quântica, o espaço-tempo nem sempre é contínuo.
Páginas relacionadas
- Dimensão
- Manifold
Perguntas e Respostas
P: De acordo com o texto, o que é espaço-tempo?
R: O espaço-tempo é um modelo matemático que conecta espaço e tempo, formando um contínuo quadridimensional conhecido como espaço de Minkowski.
P: Como a combinação de espaço e tempo ajudou a cosmologia?
R: A combinação de espaço e tempo permitiu que a cosmologia compreendesse melhor como o universo funciona tanto no nível grande, como as galáxias, quanto no nível pequeno, como os átomos.
P: Por que o uso do espaço euclidiano em vez do espaço-tempo é bom na mecânica clássica não relativística?
R: Na mecânica clássica não relativística, o uso do espaço euclidiano é bom porque o tempo é tratado como universal, com uma taxa de passagem constante que independe do estado de movimento do observador.
P: Por que o tempo é inseparável das três dimensões do espaço em um universo relativista?
R: O tempo não pode ser separado das três dimensões do espaço em um universo relativístico porque a taxa observada de passagem do tempo depende da velocidade de um objeto em relação ao observador.
P: Como a força de um campo gravitacional afeta a passagem do tempo de um objeto?
R: A força de qualquer campo gravitacional retarda a passagem do tempo para um objeto, conforme visto por um observador fora do campo.
P: Qual é o nome do continuum quadridimensional que une o espaço e o tempo?
R: O continuum quadridimensional que une o espaço e o tempo é chamado de espaço de Minkowski.
P: Como a combinação de espaço e tempo ajudou a cosmologia a entender o universo?
R: A combinação de espaço e tempo ajudou a cosmologia a entender melhor o funcionamento do universo, inclusive no nível grande, como as galáxias, e no nível pequeno, como os átomos.
Pesquise na enciclopédia