Constante Planck

Antecedentes

Símbolos usados neste artigo.
Símbolo Significado E Energia h Planck constante k Constante de Boltzmann c velocidade da luz λ comprimento de onda de radiação ν freqüência de radiação T temperatura absoluta

Entre 1670 e 1900, cientistas discutiram a natureza da luz. Alguns cientistas acreditavam que a luz consistia de muitos milhões de partículas minúsculas. Outros cientistas acreditavam que a luz era uma onda.

Luz: ondas ou partículas?

Em 1678, Christiaan Huygens escreveu o livro Traité de la lumiere ("Tratado sobre a luz"). Ele acreditava que a luz era feita de ondas. Ele disse que a luz não podia ser composta de partículas porque a luz de dois feixes não ricocheteia um sobre o outro. Em 1672, Isaac Newton escreveu o livro Opticks. Ele acreditava que a luz era composta de partículas vermelhas, amarelas e azuis que ele chamava de corpúsculos. Newton explicou isto por sua "experiência de dois prismas". O primeiro prisma quebrou a luz em cores diferentes. O segundo prisma fundiu essas cores de volta à luz branca.

Durante o século XVIII, a teoria de Newton foi a que recebeu mais atenção. Em 1803, Thomas Young descreveu a "experiência da dupla ranhura". Nesta experiência, a luz passando por duas fendas estreitas interfere em si mesma. Isto causa um padrão que mostra que a luz é feita de ondas. Durante o resto do século XIX, a teoria das ondas de luz foi a que recebeu mais atenção. Na década de 1860, James Clerk Maxwell desenvolveu equações que descreviam a radiação eletromagnética como ondas.

A teoria da radiação eletromagnética trata a luz, ondas de rádio, microondas e muitos outros tipos de ondas como a mesma coisa, exceto que elas têm comprimentos de onda diferentes. O comprimento de onda da luz que podemos ver com nossos olhos é aproximadamente entre 400 e 600 nm. O comprimento de onda das ondas de rádio varia de 10 m a 1500 m e o comprimento de onda das microondas é de cerca de 2 cm. Em um vácuo, todas as ondas eletromagnéticas viajam à velocidade da luz. A freqüência da onda eletromagnética é dada por:

ν = c λ {\i1}displaystyle {\i}nu ={\i1}frac {\i}{\i}lambda .

Os símbolos são definidos aqui.

Radiadores de corpo preto

Todas as coisas quentes emitem radiação térmica, que é a radiação eletromagnética. Para a maioria das coisas na Terra, esta radiação está na faixa infravermelha, mas algo muito quente (1000 °C ou mais), emite radiação visível, ou seja, luz. No final do século XIX, muitos cientistas estudaram os comprimentos de onda da radiação eletromagnética de radiadores de corpo negro a diferentes temperaturas.

Lei Rayleigh-Jeans

Lord Rayleigh publicou pela primeira vez as bases da lei Rayleigh-Jeans em 1900. A teoria foi baseada na teoria cinética dos gases. Sir James Jeans publicou uma teoria mais completa em 1905. A lei relaciona a quantidade e o comprimento de onda da energia eletromagnética emitida por um radiador de corpo negro a diferentes temperaturas. A equação que descreve isto é:

B λ ( T ) = 2 c k T λ 4 {\displaystyle B_{\lambda }(T)={\frac ^{\frac ^{\frac {\frac ^{\frac ^4}}}} .

Para radiação de comprimento de onda longo, os resultados previstos por esta equação corresponderam bem com os resultados práticos obtidos em um laboratório. Entretanto, para comprimentos de onda curtos (luz ultravioleta), a diferença entre teoria e prática era tão grande que ganhou o apelido de "a catástrofe ultra-violeta".

A Lei de Planck

em 1895 Wien publicou os resultados de seus estudos sobre a radiação de um corpo negro. Sua fórmula era:

B λ ( T ) = 2 h c 2 λ 5 e - h c λ k T T {\i1}displaystyle B_{\i1}(T)={\i1}frac {\i}{\i}{\i1}e^{\i}-{\i}{\i1}lambda kT}}}} .

Esta fórmula funcionou bem para radiação eletromagnética de comprimento de onda curto, mas não funcionou bem com comprimentos de onda longos.

Em 1900 Max Planck publicou os resultados de seus estudos. Ele tentou desenvolver uma expressão para a radiação de corpo negro expressa em termos de comprimento de onda, assumindo que a radiação consistia em pequenos quanta e depois ver o que acontecia se os quanta fossem feitos infinitamente pequenos. (Esta é uma abordagem matemática padrão). A expressão era:

B λ ( T ) = 2 h c 2 λ 5 1 e h c λ k T - 1 {\i1}{\i1}displaystyle B_lambda {\i}(T)={\i1}frac {\i}{\i}{\i1}{\i1}(T)={\i1}frac {\i}{\i}{\i}{\i1}frac {\i}{\i}{\i1}(T ) = 2 h c 2 λ 5 1 e h c λ k T - 1 .

Se for permitido que o comprimento de onda da luz se torne muito grande, então pode ser demonstrado que as relações Raleigh-Jeans e Planck são quase idênticas.

Ele calculou h e k e descobriu que

h = 6,55×10-27 erg-sec.

k = 1,34×10-16 erg-deg-1.

Os valores estão próximos aos valores modernos aceitos de 6,62606×10-34 e 1,38065×10-16, respectivamente. A lei Planck concorda bem com os dados experimentais, mas seu pleno significado só foi apreciado vários anos depois.

Teoria quântica da luz

Acontece que os elétrons são desalojados pelo efeito fotoelétrico se a luz atingir uma freqüência limite. Abaixo disso, não podem ser emitidos elétrons do metal. Em 1905 Albert Einstein publicou um artigo explicando o efeito. Einstein propôs que um feixe de luz não é uma onda que se propaga pelo espaço, mas uma coleção de pacotes de ondas discretas (fótons), cada uma com energia. Einstein disse que o efeito era devido a um fóton que atingia um elétron. Isto demonstrou a natureza da partícula de luz.

Einstein também descobriu que a radiação eletromagnética com um longo comprimento de onda não teve nenhum efeito. Einstein disse que isto se devia ao fato de que as "partículas" não tinham energia suficiente para perturbar os elétrons.

Plank sugeriu que a energia de cada fóton estava relacionada com a freqüência do fóton pela constante Planck. Isto poderia ser escrito matematicamente como:

E = h ν = h c λ {\displaystyle E=h\nu ={\frac {\hc}{\lambda }}} .

Plank recebeu o Prêmio Nobel em 1918, em reconhecimento aos serviços prestados ao avanço da Física por sua descoberta dos quanta energéticos. Em 1921 Einstein recebeu o Prêmio Nobel por ligar a constante de Planck ao efeito fotoelétrico.

Ilustração retirada da carta original de Newton à Royal Society (1 de janeiro de 1671 [calendário juliano]). S representa a luz do sol. A luz entre os planos BC e DE está em cores. Estas cores são recombinadas para formar a luz solar no plano GH


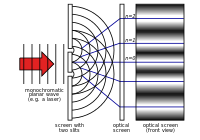
Experiência de fenda dupla de jovens


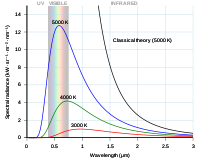
A curva de Rayleigh-Jeans e a curva de Planck traçada contra o comprimento de onda do fóton.


Conferência Solway 1911. Planck, Einstein e Jeans estão de pé. Planck é o segundo a partir da esquerda. Einstein é o segundo a partir da direita. Jeans está em quinto a partir da direita. Wien está sentado, terceiro a partir da direita.

Aplicação

A constante Planck é de importância em muitas aplicações. Algumas delas estão listadas abaixo.

Modelo Bohr do átomo

Em 1913 Niels Bohr publicou o modelo Bohr da estrutura de um átomo. Bohr disse que o momento angular dos elétrons em torno do núcleo só pode ter certos valores. Estes valores são dados pela equação

L = n h 2 π {\i} {\i1}}displaystyle L=n{\i}{\i}{\i}{\i1}

onde

L = momento angular associado a um nível.

n = número inteiro positivo.

h = constante de Planck.

O modelo Bohr do átomo pode ser usado para calcular a energia dos elétrons em cada nível. Os elétrons normalmente preenchem os estados numerados mais baixos de um átomo. Se o átomo recebe energia, por exemplo, de uma corrente elétrica, os elétrons serão excitados para um estado superior. Os elétrons cairão de volta a um estado inferior e perderão sua energia extra ao emitir um fóton. Como os níveis de energia têm valores específicos, os fótons terão níveis de energia específicos. A luz emitida desta forma pode ser dividida em diferentes cores usando um prisma. Cada elemento tem seu próprio padrão. O padrão para néon é mostrado ao lado.

O princípio da incerteza de Heisenberg

Em 1927 Werner Heisenberg publicou o princípio da incerteza. O princípio afirma que não é possível fazer uma medição sem perturbar a coisa que está sendo medida. Ele também coloca um limite ao mínimo de distúrbio causado pela realização de uma medição.

No mundo macroscópico, estes distúrbios fazem muito pouca diferença. Por exemplo, se a temperatura de um frasco de líquido for medida, o termômetro absorverá uma pequena quantidade de energia à medida que aquece. Isto causará um pequeno erro na leitura final, mas este erro é pequeno e não é importante.

Na mecânica quântica, as coisas são diferentes. Algumas medidas são feitas observando o padrão de fótons dispersos. Um exemplo é a dispersão de Compton. Se tanto a posição quanto o momento de uma partícula está sendo medida, o princípio de incerteza afirma que há um trade-off entre a precisão com que o momento é medido e a precisão com que a posição é medida. A equação que descreve este trade-off é:

Δ x Δ p ≳ h [\i1}displaystyle Delta x,{\i1}delta pgtrsim hqquad {\i1}qquad

onde

Δp = incerteza no momento.

Δx = incerteza na posição.

h = constante de Planck.

Cor dos diodos emissores de luz

No circuito elétrico mostrado à direita, a queda de voltagem através do diodo emissor de luz (LED) depende do material do LED. Para os diodos de silício, a queda é de 0,6 V. Entretanto, para os LEDs ela está entre 1,8 V e 2,7 V. Esta informação permite ao usuário calcular a constante de Planck.

A energia necessária para que um elétron salte a barreira potencial no material LED é dada por

E = Q e V L =Q_{e}V_{L},}

onde

Qe é a carga sobre um elétron.

VL é a queda de tensão através do LED.

Quando o elétron volta a decair, ele emite um fóton de luz. A energia do fóton é dada pela mesma equação utilizada no efeito fotoelétrico. Se estas equações forem combinadas, o comprimento de onda da luz e a voltagem estão relacionados por

λ = h c V L Q e {\i1}displaystyle {\i}lambda ={\i1}frac {\i}{V_{L}Q_{e}},}

A tabela abaixo pode ser calculada a partir desta relação.

Cor	Comprimento de onda (nm)	Voltagem
semáforo vermelho	650	1.89
luz verde	550	2.25
luz azul	470	2.62

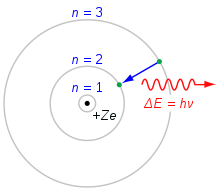
O modelo do átomo de Bohr. Um elétron que cai da casca n=3 para a casca n=2, perde energia. Esta energia é transportada como um único fóton.


Espectro visível do néon. Cada linha representa um par diferente de níveis de energia.


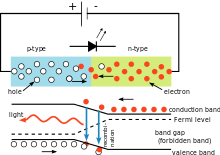
Circuito de LED simples que ilustra o uso da constante Planck. A cor da luz emitida depende da queda de tensão através do diodo. O comprimento de onda da luz pode ser calculado usando a constante de Planck.

Valor da constante Planck e a redefinição do quilograma

Desde sua descoberta, as medidas de h se tornaram muito melhores. Planck citou pela primeira vez o valor de h para ser 6,55×10-27 erg-sec. Este valor está dentro de 5% do valor atual.

A partir de 3 de março de 2014, as melhores medidas de h em unidades SI são 6,62606957×10-34 J-s. O valor equivalente em unidades cgs é 6,62606957×10-27 erg-sec. A incerteza relativa de h é de 4,4×10-8.

A constante reduzida de Planck (ħ) é um valor que às vezes é usado na mecânica quântica. Ela é definida por

ℏ = h 2 π {\i} {\i} {\i1}displaystyle {\i}hbar ={\i}frac {\i} .

As unidades Planck são às vezes usadas na mecânica quântica em vez de SI. Neste sistema a constante reduzida de Planck tem o valor 1, portanto o valor da constante de Planck é 2π.

As planchas constantes podem agora ser medidas com muito alta precisão. Isto levou o BIPM a considerar uma nova definição para o quilograma. O quilograma protótipo internacional não é mais utilizado para definir o quilograma. Ao invés disso, o BIPM define a constante de Planck para ter um valor exato. Os cientistas utilizam este valor e as definições do metro e da segunda para definir o quilograma.

 

Valor da constante teórica do Planck

A constante de Planck também pode ser derivada matematicamente:

 

h = μ 0 π 12 c 3 [ q 0 [ 0,9163 a 0 ] 2 ] 2 f 1 r 5 ⋅ s = 6,63 × 10 - 34 J ⋅ s {\i1}{\i}}{\i}{\i1}{\i}{\i}{12c^{3}}{[q_{0}}{[0,9163a_{0}} ^{2}}{f_{1r}}}{f_{5}cdot {s}=6,63 vezes 10^{-34}Jcdot s

Aqui, μ 0 {\i0} é a permeabilidade do espaço livre, c {\i1} é a velocidade da luz, q 0 {\i1} é a carga elétrica do elétron, a 0 {\i1} é o raio de Bohr, e f 1 r {\i1r é a freqüência de rotação do elétron em um átomo de hidrogênio ( f 1 r = 3.29 × 10 15 r e v / s ) {\i1r=3,29 vezes 10^{15}rev/s} . Quando estes valores constantes são substituídos pela constante teórica de Planck, o valor da constante teórica de Planck é exatamente igual ao valor experimental.

Páginas relacionadas

• Dualidade onda-partícula